
若方程 的根在区间
的根在区间 上,则
上,则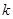 的值为( )
的值为( )
A.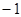 B.1 C.
B.1 C.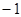 或2 D.
或2 D.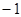 或1
或1
D
【解析】
试题分析:令f(x)=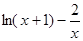 ,且x>-1,则方程
,且x>-1,则方程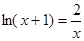 的实数根即为f(x)的零点.
的实数根即为f(x)的零点.
则当x>0时,f(x)在区间(k,k+1)(k∈Z)上单调递增,
由于f(1)=ln2-2<0,f(2)=ln3-1>0,
∴f(1)?f(2)<0,故f(x)在(1,2)上有唯一零点.
当x<0时,f(x)在区(-1,0)上也是增函数,由f(-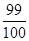 )=ln
)=ln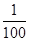 +
+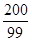 =
=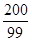 -ln100<3-lne3=0,
-ln100<3-lne3=0,
f(-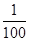 )=ln
)=ln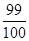 +200>200-ln1>200>0,
+200>200-ln1>200>0,
可得 f(-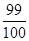 )?f(-
)?f(-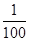 )<0,故函数f(x)在(-
)<0,故函数f(x)在(-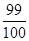 ,-
,-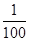 )上也有唯一零点,
)上也有唯一零点,
故f(x)在区(-1,0)上也唯一零点,此时,k=-1.
综上可得,∴k=±1,故选D.
考点:函数的零点的定义,零点存在定理。
点评:中档题,判断函数的零点所在的区间的方法,主要是零点存在定理。本题解答体现了化归与转化、分类讨论的数学思想。


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com