
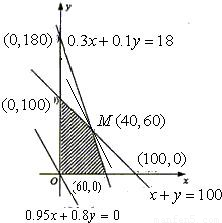
 解:设王先生分别用x万元、y万元投资线路板厂和机械加工厂两个项目,盈利为z万元.
解:设王先生分别用x万元、y万元投资线路板厂和机械加工厂两个项目,盈利为z万元.
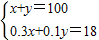


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题12分)某乡镇为了盘活资本,优化组合,决定引进资本拯救出现严重亏损的企业。长年在外经商的王先生为了回报家乡,决定投资线路板厂和机械加工厂。王先生经过预算,如果引进新技术在优化管理的情况下,线路板厂和机械加工厂可能的最大盈利率分别为95﹪和80﹪,可能的最大亏损率分别为30﹪和10﹪。由于金融危机的影响,王先生决定最多出资100万元引进新技术,要求确保可能的资金亏损不超过18万元.问王先生对线路板厂和机械加工厂各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省名校高三数学一轮复习综合测试(五)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三下学期数学单元测试5-文科 题型:解答题
某乡镇为了盘活资本,优化组合,决定引进资本拯救出现严重亏损的企业。长年在外经商的王先生为了回报家乡,决定投资线路板厂和机械加工厂。王先生经过预算,如果引进新技术在优化管理的情况下,线路板厂和机械加工厂可能的最大盈利率分别为95﹪和80﹪,可能的最大亏损率分别为30﹪和10﹪。由于金融危机的影响,王先生决定最多出资100万元引进新技术,要求确保可能的资金亏损不超过18万元.问王先生对线路板厂和机械加工厂各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com