
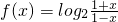
 >0,
>0,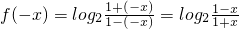 =
=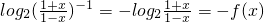 ,
,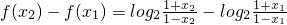
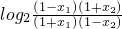 .
.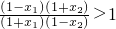 ,
,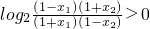 ,
,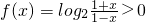 ,
, ,
,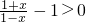 ,
,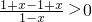 ,
,

科目:高中数学 来源: 题型:013
已知命题:p:一次函数的图象是一条直线;命题q:函数y=ax2+bx+c(a,b,c为常数)的图象是一条抛物线,则下面四种形式的复合命题中真命题是
①非p ②非q ③p或q ④p且q
A.①②
B.①③
C.②③
D.③④
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
①非p ②非q ③p或q ④p且q
A.①②
B.①③
C.②③
D.③④
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省十二校高三第一次联考数学理卷 题型:填空题
已知函数f(x)=(x2-x-)eax(a≠0).
(1)曲线y=f(x)在点A(0,f(0))处的切线方程为 ;
(2)当a>0时,若不等式f(x)+≥0对x∈[-,+∞)恒成立,则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:辽宁省抚顺市六校联合体2009-2010学年度高三二模(数学理)试题 题型:选择题
已知命题 :函数
:函数 的图像必过定点
的图像必过定点 ;命题
;命题 的图像关于
的图像关于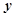 轴对称,则函数
轴对称,则函数 关于直线
关于直线 对称,那么
(
)
对称,那么
(
)
A 、 为真
B、
为真
B、 为假
为假
C、 D、
D、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com