
 ,定义使f(1)•f(2)…f(k)为整数的数k(k∈N*)叫做企盼数,则在区间[1,2011]内这样的企盼数共有 个.
,定义使f(1)•f(2)…f(k)为整数的数k(k∈N*)叫做企盼数,则在区间[1,2011]内这样的企盼数共有 个.  •
• …
… =
= =log2(k+2),
=log2(k+2), 求得(1)•f(2)…f(k)=log2(k+2)是解答本题的关键,属于难题.
求得(1)•f(2)…f(k)=log2(k+2)是解答本题的关键,属于难题. 

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
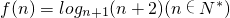 ,定义使f(1)•f(2)…f(k)为整数的数k(k∈N*)叫做企盼数,则在区间[1,2011]内这样的企盼数共有________个.
,定义使f(1)•f(2)…f(k)为整数的数k(k∈N*)叫做企盼数,则在区间[1,2011]内这样的企盼数共有________个.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
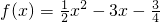 .定义函数f(x)与实数m的一种符号运算为m?f(x)=f(x)•[f(x+m)-f(x)].
.定义函数f(x)与实数m的一种符号运算为m?f(x)=f(x)•[f(x+m)-f(x)].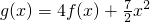 ,求g(x)在区间[0,4]上的最大值与最小值.
,求g(x)在区间[0,4]上的最大值与最小值.查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省中山市高二(上)期末数学试卷(理科)(解析版) 题型:解答题
 .定义函数f(x)与实数m的一种符号运算为m?f(x)=f(x)•[f(x+m)-f(x)].
.定义函数f(x)与实数m的一种符号运算为m?f(x)=f(x)•[f(x+m)-f(x)]. ,求g(x)在区间[0,4]上的最大值与最小值;
,求g(x)在区间[0,4]上的最大值与最小值; .若存在,求出其通项;若不存在,请说明理由.
.若存在,求出其通项;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com