
已知二次函数 满足
满足 ,且
,且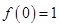 。
。
(1)求 的解析式;
的解析式;
(2)当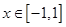 时,方程
时,方程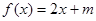 有解,求实数
有解,求实数 的取值范围;
的取值范围;
(3)设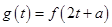 ,
,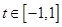 ,求
,求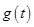 的最大值.
的最大值.
解析试题分析:(1)设出二次函数的一般形式后,代入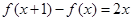 ,化简后根据多项式相等,各系数相等即可求出
,化简后根据多项式相等,各系数相等即可求出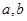 及
及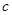 的值,即可确定出
的值,即可确定出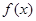 的解析式;
的解析式;
(2)不等式有解即为把不等式变为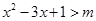 有解,令
有解,令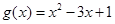 ,求出
,求出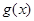 在区间
在区间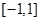 上的值域,即可得到
上的值域,即可得到 的取值范围,
的取值范围,
(3)把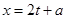 代入
代入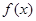 的解析式中即可表示出
的解析式中即可表示出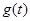 的函数关系式,由二次函数求对称轴的方法表示出
的函数关系式,由二次函数求对称轴的方法表示出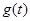 的对称轴,根据对称轴大于等于
的对称轴,根据对称轴大于等于 和小于
和小于 ,分两种情况考虑,分别画出相应的函数图象,根据函数的图象即可分别得到
,分两种情况考虑,分别画出相应的函数图象,根据函数的图象即可分别得到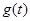 的最大值,并求出相应
的最大值,并求出相应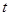 的范围,联立即可得到
的范围,联立即可得到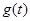 最大值与
最大值与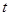 的分段函数解析式.
的分段函数解析式.
试题解析:解:(1)设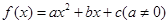
代入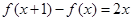 和
和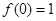 [来源:学#科#网]
[来源:学#科#网]
并化简得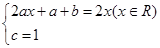 ,
,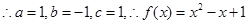
(2)当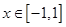 时,方程
时,方程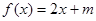 有解
有解
即方程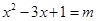 在上
在上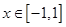 有解
有解
令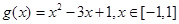 ,则
,则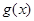 的值域是
的值域是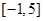
故 的取值范围是
的取值范围是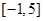
(3)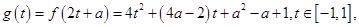
对称轴是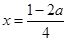 。
。
①当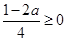 时,即
时,即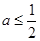 时
时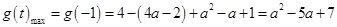 ;
;
② 当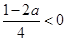 时,即
时,即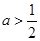 时,
时,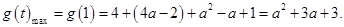
综上所述:。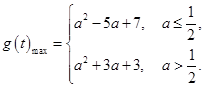
考点:考查函数的解析式,二次函数的图象与性质及不等式恒成立时所满足的条件,考查了分类讨论的数学思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
如果函数 满足在集合
满足在集合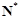 上的值域仍是集合
上的值域仍是集合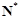 ,则把函数
,则把函数 称为N函数.
称为N函数.
例如: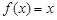 就是N函数.
就是N函数.
(Ⅰ)判断下列函数:①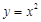 ,②
,②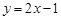 ,③
,③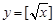 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果);
(Ⅱ)判断函数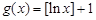 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;
(Ⅲ)证明:对于任意实数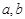 ,函数
,函数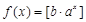 都不是N函数.
都不是N函数.
(注:“ ”表示不超过
”表示不超过 的最大整数)
的最大整数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在不考虑空气阻力的情况下,火箭的最大速度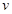 (单位:
(单位: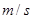 )和燃料的质量
)和燃料的质量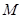 (单位:
(单位: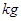 ),火箭(除燃料外)的质量
),火箭(除燃料外)的质量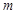 (单位:
(单位: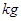 )满足
)满足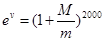 .(
.(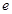 为自然对数的底)
为自然对数的底)
(Ⅰ)当燃料质量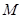 为火箭(除燃料外)质量
为火箭(除燃料外)质量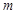 两倍时,求火箭的最大速度(单位:
两倍时,求火箭的最大速度(单位: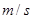 );
);
(Ⅱ)当燃料质量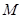 为火箭(除燃料外)质量
为火箭(除燃料外)质量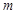 多少倍时,火箭的最大速度可以达到8
多少倍时,火箭的最大速度可以达到8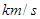 .(结果精确到个位,数据:
.(结果精确到个位,数据: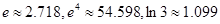 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是某重点中学学校运动场平面图,运动场总面积15000平方米,运动场是由一个矩形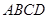 和分别以
和分别以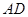 、
、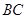 为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,
为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,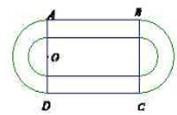
(Ⅰ)设半圆的半径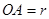 (米),写出塑胶跑道面积
(米),写出塑胶跑道面积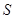 与
与 的函数关系式
的函数关系式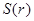 ;
;
(Ⅱ)由于受运动场两侧看台限制, 的范围为
的范围为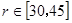 ,问当
,问当 为何值时,运动场造价最低(第2问
为何值时,运动场造价最低(第2问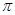 取3近似计算).
取3近似计算).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 ,且不等式
,且不等式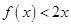 的解集为
的解集为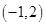 .
.
(1)方程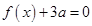 有两个相等的实根,求
有两个相等的实根,求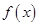 的解析式;
的解析式;
(2)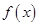 的最小值不大于
的最小值不大于 ,求实数
,求实数 的取值范围;
的取值范围;
(3) 如何取值时,函数
如何取值时,函数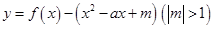 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com