
集合A={x|︱x+3|+|x-4|≤9},B{x|x=4t+ -6,t∈(0,+∞) },则集合A∩B= .
-6,t∈(0,+∞) },则集合A∩B= .
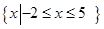
解析试题分析:先解|x+3|+|x-4|≤9。将-3、4看成两个分界点,
则分别在x≤-3、-3<x<4、x≥4三个取值范围内分析
当x≤-3时,-(x+3)-(x-4)≤9
化简得:x≥-4,即,-4≤x≤-3 ;
当-3<x<4时,x+3-(x-4)≤9
化简得:7≤9(恒成立)
则x>-3
当x≥4时,x+3+x-4≤9
化简得:x≤5
则,4≤x≤5
综上知:-4≤x≤5
故:A={x|-4≤x≤5}
再确定x=4t+ -6,t∈(0,+∞)的值域,由均值定理得4t+
-6,t∈(0,+∞)的值域,由均值定理得4t+
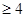 ,所以x
,所以x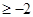 :B={x|x
:B={x|x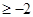 }
}
故A∩B=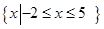 。
。
考点:本题主要考查集合的运算,均值不等式的应用,绝对值不等式的解法。
点评:综合题,利用绝对值的几何意义解不等式,形象直观,易懂。“对号函数”的值域,可应用单调性讨论,也可利用均值定理。


 考前必练系列答案
考前必练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com