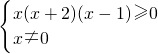解:(1)原不等式可化为3x
2-19x+6≤0
?(3x-1)(x-6)≤0?(x-

)(x-6)≤0.
可化为:
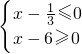
或
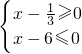
,
解得:

≤x≤6,
∴原不等式的解集为{x|

≤x≤6};
(2)原不等式可化为x+1-

≥0?

≥0
?

≥0?
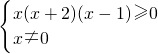
如图所示:

∴原不等式的解集为{x|-2≤x<0,或x≥1}.
分析:(1)把不等式右边移项到左边,因式分解得到两个式子乘积小于等于0,得到两式子异号,化为两个不等式组,求出不等式组的解集即可得到原不等式的解集;
(2)把不等式的右边移项到左边并通分,因式分解后转为为x(x+2)(x-1)大于等于0且x不等于0,根据数轴即可得到原不等式的解集.
点评:此题考查了一元二次不等式的解法,考查了转化的思想及数形结合的思想,是一道基础题.

 .
. )(x-6)≤0.
)(x-6)≤0.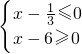 或
或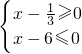 ,
, ≤x≤6,
≤x≤6, ≤x≤6};
≤x≤6}; ≥0?
≥0? ≥0
≥0 ≥0?
≥0?