
已知椭圆C1: ,抛物线C2:
,抛物线C2: ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.
(Ⅰ)当AB⊥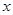 轴时,求
轴时,求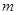 、
、 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)是否存在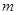 、
、 的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的
的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的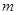 、
、 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅰ)m=0,
 .此时C2的焦点坐标为(
.此时C2的焦点坐标为( ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.
(II)满足条件的 、
、 存在,且
存在,且 或
或 ,
, .
.
【解析】
试题分析:(Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为: x =1,从而点A的坐标为(1, )或(1,-
)或(1,- ). 因为点A在抛物线上.所以
). 因为点A在抛物线上.所以 ,即
,即 .此时C2的焦点坐标为(
.此时C2的焦点坐标为( ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.
(II):
假设存在 、
、 的值使
的值使 的焦点恰在直线AB上,由(I)知直线AB的斜率存在,故可设直线AB的方程为
的焦点恰在直线AB上,由(I)知直线AB的斜率存在,故可设直线AB的方程为 .
.
由 消去
消去 得
得 …①
…①

设A、B的坐标分别为(x1,y1), (x2,y2),
则x1,x2是方程①的两根,x1+x2= .
.
由 消去y得
消去y得 . ………………②
. ………………②
因为C2的焦点 在直线
在直线 上,
上,
所以 ,即
,即 .代入②有
.代入②有 .
.
即 . …………………③
. …………………③
由于x1,x2也是方程③的两根,所以x1+x2= .
.
从而 =
= . 解得
. 解得 ……………………④
……………………④
又AB过C1,C2的焦点,所以
 ,
,
则 …………………………………⑤
…………………………………⑤
由④、⑤式得 ,即
,即 .
.
解得 于是
于是
因为C2的焦点 在直线
在直线 上,所以
上,所以 .
.

 或
或 .
.
由上知,满足条件的 、
、 存在,且
存在,且 或
或 ,
, .
.
考点:本题主要考查直线方程,椭圆及抛物线的几何性质,直线与抛物线的位置关系。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题解答过程中,主要运用了抛物线的几何性质。结合抛物线的焦半径公式,建立了k的方程。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| |AB| |
| |CD| |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C1:![]() ,抛物线C2:
,抛物线C2:![]() ,
,
且C1、C2的公共弦AB过椭圆C1的右焦点.
(Ⅰ)当AB⊥![]() 轴时,求
轴时,求![]() 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)是否存在![]() 的值,使抛物线C2的焦点恰在直线AB上?若存在,
的值,使抛物线C2的焦点恰在直线AB上?若存在,
求出符合条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com