练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，直四棱柱A1B1C1D1－ABCD的高为3，底面是边长为4，且∠DAB＝60°的菱形，O是AC与BD的交点，O1是A1C1与B1D1的交点．

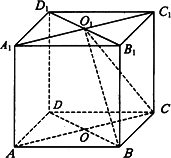
    (Ⅰ)求二面角O1－BC－D的大小；

    (Ⅱ)求点A到平面O1BC的距离．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

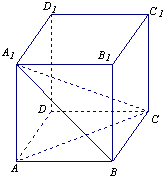    如图，直四棱柱ABCD-A1B1C1D1中，平面A1BC⊥平面A1ABB1，AB=BC=2，AA1=2
    		2
    ．
    （1）求证：BC⊥平面A1ABB1；
    （2）求直线A1B与平面A1AC成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源：湖北省荆州中学2008高考复习立体几何基础题题库二(有详细答案)人教版 人教版 题型：047

    求证：底面是梯形的直棱柱的体积，等于两个平行侧面面积的和与这两个侧面间距离的积的一半．

    已知：直四棱柱A1C，如图，它的底面AC为梯形．DC∥AB，侧面A1B与侧面D1C的距离为h．

    求证：＝(＋)×h

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (本小题满分12分)

    如图，直四棱柱ABCD－A1B1C1D1中，底面ABCD是边长为a的   

    菱形，且，侧棱AA1长等于3a，O为底面ABCD对

    角线的交点.

    （1）求证：OA1∥平面B1CD1；

    （2）求异面直线AC与A1B所成的角；

    （3）在棱上取一点F，问AF为何值时，C1F⊥平面BDF？

    查看答案和解析>>

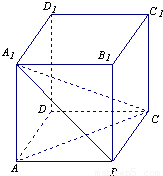
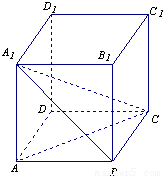
    科目：高中数学 来源：2012-2013学年黑龙江省哈尔滨六中高二（上）期中数学试卷（理科）（解析版） 题型：解答题

    如图，直四棱柱ABCD-A1B1C1D1中，平面A1BC⊥平面A1ABB1，AB=BC=2，．
    （1）求证：BC⊥平面A1ABB1；
    （2）求直线A1B与平面A1AC成角的正弦值．

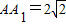    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年黑龙江省哈尔滨六中高二（上）期中数学试卷（理科）（解析版） 题型：解答题

    如图，直四棱柱ABCD-A1B1C1D1中，平面A1BC⊥平面A1ABB1，AB=BC=2，．
    （1）求证：BC⊥平面A1ABB1；
    （2）求直线A1B与平面A1AC成角的正弦值．

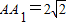    查看答案和解析>>

    同步练习册答案