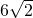练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    过抛物线y2=8x的焦点F的直线交抛物线于A，B两点，O为坐标原点，若|BF|=3，则△AOB的面积为


    1. A.
      数学公式
    2. B.
      数学公式
    3. C.
      数学公式
    4. D.
      数学公式
    A
    分析：设∠BFx=θ（0＜θ＜π），利用BF|=3，可得点B到准线l：x=-2的距离为3，从而可得cosθ的值，进而可求|AF|，|AB|，由此可求△AOB的面积．
    解答：设∠BFx=θ（0＜θ＜π）及|AF|=m，
    ∵|BF|=3，
    ∴点B到准线l：x=-2的距离为3
    ∴4+3cosθ=3
    ∴cosθ=-
    ∵m=4+mcos（π-θ）
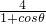
    ∴m==6
    ∴△AOB的面积为S=×|OF|×|AB|×sinθ=×2×9×=
    故选A．
    点评：本题考查抛物线的定义，考查三角形的面积的计算，确定抛物线的弦长是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    7、过抛物线y2=8x的焦点，作直线交抛物线于A（x1，y1），B（x2，y2）两点，若x1+x2=6，则|AB|长为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若椭圆
    x2
    a2
    +
    y2
    b2
    =1    过抛物线y2=8x的焦点，且与双曲线x2-y2=1有相同的焦点，则该椭圆的方程为
    x2
    4
    +
    y2
    2
    =1
    x2
    4
    +
    y2
    2
    =1
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•虹口区一模）过抛物线y2=8x的焦点作弦AB，点A（x1，y1），B（x2，y2），且x1+x2=10，则|AB|=
    14
    14
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    过抛物线y2=8x的焦点F的直线交抛物线于A，B两点，O为坐标原点，若|BF|=3，则△AOB的面积为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若椭圆C：
    x2
    m2
    +
    y2
    n2
    =1    过抛物线y2=8x的焦点，且与双曲线x2-y2=-1有相同的焦点，则该椭圆的方程是（　　）

    查看答案和解析>>

    同步练习册答案