
���� ���$\overrightarrow{a}•\overrightarrow{b}$����$\overrightarrow{c}$=2x$\overrightarrow{a}$+y$\overrightarrow{b}$����ƽ�������û�������ʽ�ó�xy�ķ�Χ��
��� �⣺$\overrightarrow{a}•\overrightarrow{b}$=1��1��cos60��=$\frac{1}{2}$����$\overrightarrow{c}$=2x$\overrightarrow{a}$+y$\overrightarrow{b}$�ǵ�λ��������4x2+y2+4xy$\overrightarrow{a}•\overrightarrow{b}$=1��
��4x2+y2=1-2xy��4xy����xy��$\frac{1}{6}$��
�ʴ�Ϊ��$\frac{1}{6}$��
���� ���⿼����ƽ���������������㣬��������ʽ��Ӧ�ã����ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
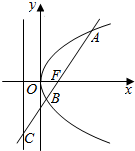 ��ͼ��ֱ��l��������y2=4x�Ľ���F�ҷֱ�������������A��B��C����$\frac{BF}{BC}$=$\frac{\sqrt{5}}{5}$����|AB|=5��
��ͼ��ֱ��l��������y2=4x�Ľ���F�ҷֱ�������������A��B��C����$\frac{BF}{BC}$=$\frac{\sqrt{5}}{5}$����|AB|=5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 15��1+$\sqrt{2}$�� | B�� | 15��1+$\frac{\sqrt{2}}{2}$�� | C�� | 15��$\sqrt{2}$-1����15��1-$\frac{\sqrt{2}}{2}$�� | D�� | 15��1+$\sqrt{2}$����15��1+$\frac{\sqrt{2}}{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
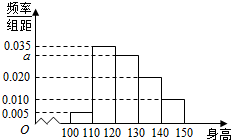 ��ijСѧ�����ȡ200��ͬѧ�������ǵ����ߣ���λ�����ף����ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ������Ҫ��������[120��130����[130��140����[140��150]�����ڵ�ѧ���У��÷ֲ�����ķ���ѡȡ36�˲μ�һ�������������[140��150]�ڵ�ѧ����ѡȡ������ӦΪ��������
��ijСѧ�����ȡ200��ͬѧ�������ǵ����ߣ���λ�����ף����ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ������Ҫ��������[120��130����[130��140����[140��150]�����ڵ�ѧ���У��÷ֲ�����ķ���ѡȡ36�˲μ�һ�������������[140��150]�ڵ�ѧ����ѡȡ������ӦΪ��������| A�� | 3 | B�� | 6 | C�� | 9 | D�� | 12 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com