
【题目】如图1,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 与
与![]() 的交点,以
的交点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() ,如图2.
,如图2.
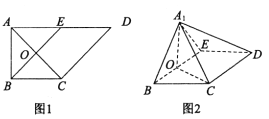
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)根据正方形的性质可得![]() ,由勾股定理可得
,由勾股定理可得![]() .可得
.可得![]() 平面
平面![]() ,由面面垂直的判定定理即可证明平面
,由面面垂直的判定定理即可证明平面![]() 平面
平面![]() ;(2)由(1)知
;(2)由(1)知![]() 互相垂直,以
互相垂直,以![]() 为轴建立空间坐标系,
为轴建立空间坐标系,![]() 为平面
为平面![]() 的法向量,利用向量垂直数量积为零列方程求出平面
的法向量,利用向量垂直数量积为零列方程求出平面![]() 的法向量,利用空间向量夹角余弦公式可求得二面角
的法向量,利用空间向量夹角余弦公式可求得二面角![]() 的余弦值.
的余弦值.
(1)在图1中,因为![]() ,
,![]() ,
,![]() ,
,
![]() 是
是![]() 的中点,,
的中点,,
所以四边形![]() 为正方形,
为正方形,
所以![]() ,
,![]()
即在图2中,![]() ,
,![]() ,
,![]() .
.
又因为![]() ,所以在
,所以在![]() 中,
中,![]() ,
,
所以![]() .
.
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由(1)知![]() 互相垂直,分别以
互相垂直,分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,如图所示,
轴建立空间直角坐标系,如图所示,

因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则 得
得![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,即
,即![]() ,
,
由(1)平面![]() 平面
平面![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 为平面
为平面![]() 的法向量,
的法向量,
所以 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(2)(几何法)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.

因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 就是二面角
就是二面角![]() 的平面角.
的平面角.
又![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:高中数学 来源: 题型:
【题目】渔民出海打鱼,为了保证获得的鱼新鲜,鱼被打上岸后,要在最短的时间内将其分拣、冷藏,若不及时处理,打上来的鱼很快地失去新鲜度(以鱼肉内的三甲胺量的多少来确定鱼的新鲜度.三甲胺是一种挥发性碱性氨,是氨的衍生物,它是由细菌分解产生的.三甲胺量积聚就表明鱼的新鲜度下降,鱼体开始变质进而腐败).已知某种鱼失去的新鲜度![]() 与其出海后时间
与其出海后时间![]() (分)满足的函数关系式为
(分)满足的函数关系式为![]() .若出海后10分钟,这种鱼失去的新鲜度为10%,出海后20分钟,这种鱼失去的新鲜度为20%,那么若不及时处理,打上来的这种鱼在多长时间后开始失去全部新鲜度(已知
.若出海后10分钟,这种鱼失去的新鲜度为10%,出海后20分钟,这种鱼失去的新鲜度为20%,那么若不及时处理,打上来的这种鱼在多长时间后开始失去全部新鲜度(已知![]() ,结果取整数)( )
,结果取整数)( )
A.33分钟B.40分钟C.43分钟D.50分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与上、下顶点构成直角三角形,以椭圆
的一个焦点与上、下顶点构成直角三角形,以椭圆![]() 的长轴长为直径的圆与直线
的长轴长为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点且不平行于![]() 轴的动直线与椭圆
轴的动直线与椭圆![]() 相交于
相交于![]() 两点,探究在
两点,探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区进行疾病普查,为此要检验每一人的血液,如果当地有![]() 人,若逐个检验就需要检验
人,若逐个检验就需要检验![]() 次,为了减少检验的工作量,我们把受检验者分组,假设每组有
次,为了减少检验的工作量,我们把受检验者分组,假设每组有![]() 个人,把这个
个人,把这个![]() 个人的血液混合在一起检验,若检验结果为阴性,这
个人的血液混合在一起检验,若检验结果为阴性,这![]() 个人的血液全为阴性,因而这
个人的血液全为阴性,因而这![]() 个人只要检验一次就够了,如果为阳性,为了明确这个
个人只要检验一次就够了,如果为阳性,为了明确这个![]() 个人中究竟是哪几个人为阳性,就要对这
个人中究竟是哪几个人为阳性,就要对这![]() 个人再逐个进行检验,这时
个人再逐个进行检验,这时![]() 个人的检验次数为
个人的检验次数为![]() 次.假设在接受检验的人群中,每个人的检验结果是阳性还是阴性是独立的,且每个人是阳性结果的概率为
次.假设在接受检验的人群中,每个人的检验结果是阳性还是阴性是独立的,且每个人是阳性结果的概率为![]() .
.
(Ⅰ)为熟悉检验流程,先对3个人进行逐个检验,若![]() ,求3人中恰好有1人检测结果为阳性的概率;
,求3人中恰好有1人检测结果为阳性的概率;
(Ⅱ)设![]() 为
为![]() 个人一组混合检验时每个人的血需要检验的次数.
个人一组混合检验时每个人的血需要检验的次数.
①当![]() ,
,![]() 时,求
时,求![]() 的分布列;
的分布列;
②是运用统计概率的相关知识,求当![]() 和
和![]() 满足什么关系时,用分组的办法能减少检验次数.
满足什么关系时,用分组的办法能减少检验次数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有男生27名,女生18名,用分层抽样的方法从该班中抽取5名学生去敬老院参加献爱心活动.
(1)求从该班男生、女生中分别抽取的人数;
(2)为协助敬老院做好卫生清扫工作,从参加活动的5名学生中随机抽取2名,求这2名学生均为女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造.根据史书的记载和考古材料的发现,古代的算筹实际上是一根根同样长短和粗细的小棍子,一般长为![]() ,径粗
,径粗![]() ,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带.需要记数和计算的时候,就把它们取出来,放在桌上、炕上或地上都能摆弄.在算筹计数法中,以纵横两种排列方式来表示数字.如图,是利用算筹表示数1~9的一种方法.例如:3可表示为“
,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带.需要记数和计算的时候,就把它们取出来,放在桌上、炕上或地上都能摆弄.在算筹计数法中,以纵横两种排列方式来表示数字.如图,是利用算筹表示数1~9的一种方法.例如:3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”,现有6根算筹,据此表示方法,若算筹不能剩余,则用这6根算筹能表示的两位数的个数为( )
”,现有6根算筹,据此表示方法,若算筹不能剩余,则用这6根算筹能表示的两位数的个数为( )
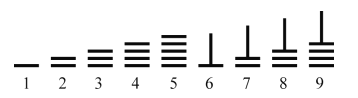
A.13B.14C.15D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非空集合![]() 关于运算
关于运算![]() 满足:① 对任意
满足:① 对任意![]() ,都有
,都有![]() ;② 存在
;② 存在![]() 使对一切
使对一切![]() 都有
都有![]() ,则称
,则称![]() 是关于运算
是关于运算![]() 的融洽集,现有下列集合及运算:
的融洽集,现有下列集合及运算:
①![]() 是非负整数集,
是非负整数集,![]() 运算:实数的加法;
运算:实数的加法;
②![]() 是偶数集,
是偶数集,![]() 运算:实数的乘法;
运算:实数的乘法;
③![]() 是所有二次三项式组成的集合,
是所有二次三项式组成的集合,![]() 运算:多项式的乘法;
运算:多项式的乘法;
④![]() ,
,![]() 运算:实数的乘法;
运算:实数的乘法;
其中为融洽集的是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的A产品被检测出其中一项质量指标存在问题,该企业为了检查生产A产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品,表格是甲流水线样本的频数分布表,图形是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品,表格是甲流水线样本的频数分布表,图形是乙流水线样本的频率分布直方图.
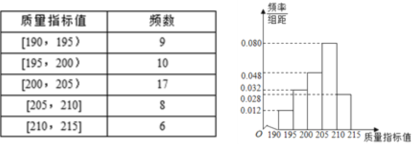
(1)根据图形,估计乙流水线生产的A产品的该质量指标值的中位数;
(2)设某个月内甲、乙两条流水线均生产了3000件产品,若将频率视为概率,则甲、乙两条流水线生产出的合格产品分别约为多少件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义域为
是定义域为![]() 的奇函数.
的奇函数.
(1)若![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 恒成立的实数
恒成立的实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 的图象过点
的图象过点![]() ,是否存在正数
,是否存在正数![]() ,使函数
,使函数![]() 在
在![]() 上的最大值为0?若存在,求出
上的最大值为0?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com