
|
| 1 |
| 2 |
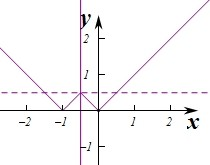
A、(0,
| ||||
B、(0,
| ||||
| C、(0,1) | ||||
| D、(0,1)∪(1,+∞) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 混合 | 烹调 | 包装 | |
| A | 1 | 5 | 3 |
| B | 2 | 4 | 1 |
查看答案和解析>>
科目:高中数学 来源:陕西省渭南市高新中学2011-2012学年高二上学期期中考试数学试题 题型:044
某糖果厂生产A、B两种糖果,A种糖果每箱可获利润40元,B种糖果每箱可获利润50元.其生产过程分混合、烹调、包装三道工序.下表为每箱糖果生产过程中所需平均时间(单位:min).
每种糖果的生产过程中,混合的设备至多用机器12 h,烹调的设备最多只能用机器30 h,包装的设备最多只能用机器15 h,每种糖果各生产多少箱可获得最大利润?
查看答案和解析>>
科目:高中数学 来源:2013届陕西省渭南市高二上学期期中考试数学试卷 题型:解答题
某糖果厂生产A、B两种糖果,A种糖果每箱可获利润40元,B种糖果每箱可获利润50元.其生产过程分混合、烹调、包装三道工序.下表为每箱糖果生产过程中所需平均时间(单位:min).
|
|
混合 |
烹调 |
包装 |
|
A |
1 |
5 |
3 |
|
B |
2 |
4 |
1 |
每种糖果的生产过程中,混合的设备至多用机器12 h,烹调的设备最多只能用机器30 h,包装的设备最多只能用机器15 h,每种糖果各生产多少箱可获得最大利润?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西省咸阳市彩虹中学高二(上)期中数学试卷(文科)(解析版) 题型:解答题
| 混合 | 烹调 | 包装 | |
| A | 1 | 5 | 3 |
| B | 2 | 4 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com