
已知三次波函数f ( x )的导函数为f′( x ),f′( 1 ) = 0 , f′(2 ) = 3 , f′( 3 ) = 12 .
(1)求f ( x ) f ( 0 )的表达式;
(2)若对任意的x∈[ 1 , 4 ],都有![]() 成立,求
成立,求![]() 的取值范围。
的取值范围。
解:(1)设f ( x ) = ax3 + bx2 + cx + d . 则f′( x ) = 3ax2 + 2bx + c ,
于是有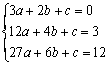
∴![]() 故f ( x ) f ( 0 ) = x3 3x2 + 3x
故f ( x ) f ( 0 ) = x3 3x2 + 3x
(2)由(1)得f′( x ) = 3x2 6x + 3 . 对任意的x∈[ 1 , 4 ], f ( x )>f′( x )
等价于f ( x ) f′( x ) = x3 6x2 + 9x + f ( 0 ) 3 >0,
令F ( x ) = x3 + 6x2 9x + 3 ,
则f ( 0 )>F ( x ) = x3 + 6x2 9x + 3
因为F′( x ) = 3x2 + 12x 9 当x∈![]() 时,F′( x )<0;
时,F′( x )<0;
当x = 1 或3时,F′( x ) = 0
当x∈( 1 , 3 )时,F′( x )>0
当x∈![]() 时,F′( x )<0
时,F′( x )<0
又F ( 1 )>F ( 3 )
所以F ( x )在[ 1 ,4]上的最大值为F ( 1 ) = 19
故f ( 0 )的取值范围是(19,+∞)


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com