
(本小题满分12分)若实数a>0且a≠2,函数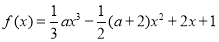 .
.
(1)证明函数f(x)在x=1处取得极值,并求出函数f(x)的单调区间;
(2)若在区间(0,+∞)上至少存在一点x0,使得f(x0)<1成立,求实数a的取值范围.
(1)见解析;(2)(0,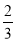 )∪(6,+∞)
)∪(6,+∞)
【解析】
试题分析:(1)只需证明x=1是导函数的零点,进而通过对a的讨论,可求出单调区间;(2)只需在(0,+∞)上f(x)最小值<1即可.
试题解析:(1)∵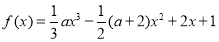
∴f '(x)=ax2-(a+2)x+2=a(x-1)(x-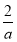 )
)
当a>2时,0<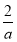 <1,列表如下:
<1,列表如下:
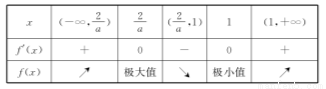
∴函数f(x)在x=1处取得极小值,
f(x)的单调递增区间是(-∞,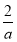 )和(1,+∞),单调递减区间是(
)和(1,+∞),单调递减区间是(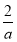 ,1).
,1).
当0<a<2时,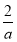 >1,列表如下:
>1,列表如下:
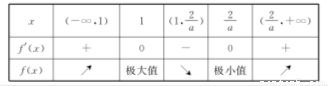
∴函数f(x)在x=1处取得极大值
f(x)的单调递增区间是(-∞,1)和(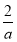 ,+∞),单调递减区间是(1,
,+∞),单调递减区间是(1,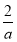 ).
).
(2)因为f(0)=1,由(1)知要使在区间(0,+∞)上至少存在一点x0,使得f(x0)<1成立,只需在区间(0,+∞)上f(x)极小值<1即可
当a>2时,f(x)极小值=f(1)=2-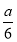 <1,所以a>6.
<1,所以a>6.
当0<a<2时,f(x)极小值=f(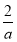 )=1+
)=1+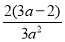 <1,解得0<a<
<1,解得0<a<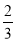
综上所述,实数a的取值范围是(0,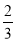 )∪(6,+∞)
)∪(6,+∞)
考点:利用导数研究函数的单调性,极值,不等式恒成立问题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考文科数学试卷(解析版) 题型:解答题
已知函数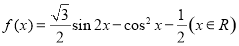
(1)当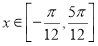 时,求函数
时,求函数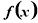 取得最大值和最小值时
取得最大值和最小值时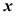 的值;
的值;
(2)设锐角△ABC的内角A、B、C的对应边分别是a,b,c,且a=1,c∈N*,若向量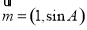 与向量
与向量 平行,求c的值.
平行,求c的值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省高三10月月考理科数学试卷(解析版) 题型:选择题
已知数列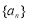 的前
的前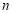 项和
项和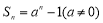 ,则数列
,则数列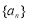 ( )
( )
A.一定是等差数列
B.一定是等比数列
C.或者是等差数列,或者是等比数列
D.既不可能是等差数列,也不可能是等比数列
查看答案和解析>>
科目:高中数学 来源:2015届四川省高三10月月考文科数学试卷(解析版) 题型:选择题
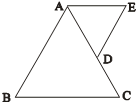
如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中, 的取值范围是( )
的取值范围是( )
A.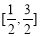 B.
B.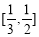 C.
C. D.
D.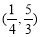
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:填空题
已知x>-1,y>0且满足x+2y=1,则 的最小值为_____________.
的最小值为_____________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:选择题
某程序框图如图所示,若输出的S=57,则判断框内应填( )
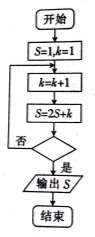
A、k>4? B、k>5? C、k>6? D、k>7?
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:填空题
已知向量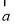 =(1,1),
=(1,1),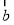 =(-1,k),(2
=(-1,k),(2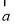 +
+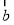 )·
)·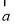 =5,则实数k=__________.
=5,则实数k=__________.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试文科数学试卷(解析版) 题型:填空题
已知直线l⊥平面α,直线 m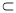 平面β,有下列四个命题:①若α∥β,则 l⊥ m ;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确命题序号是 .
平面β,有下列四个命题:①若α∥β,则 l⊥ m ;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确命题序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com