Question

（08年全国卷Ⅰ理）（本小题满分12分）

四棱锥中，底面为矩形，侧面底面，，，．

（Ⅰ）证明：；

（Ⅱ）设与平面所成的角为，求二面角的大小．

Answer 1

【解析】 解法一：

（Ⅰ）作，垂足为，连接，

由题设知，底面，且为的中点，

由知，，

从而，于是．

由三垂线定理知，．

（Ⅱ）由题意，，所以侧面，

又侧面，所以侧面侧面，

作，垂足为，连接，则平面．

故为与平面所成的角，．

由，得

又，因而，所以为等边三角形．

作，垂足为，连接．

由（Ⅰ）知，，又，

故平面，，是二面角的平面角．

，，

，，

则，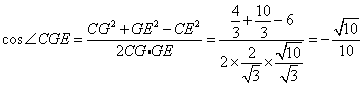

二面角为．

解法二：

（Ⅰ）作，垂足为，则底面，且为的中点，

以为坐标原点，射线为轴正方向，建立如图所示的直角坐标系．

设．由已知条件有

，

．

所以，得．

 

（Ⅱ）作，垂足为，连接．

设，则，

．

故．又，所以平面，

是与平面所成的角，．

由，得．

又，所以，所以为等边三角形，因此．

作，垂足为，连接．在中，求得；

故　　．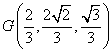

　　　

又　　，

　　　．

所以与的夹角等于二面角的平面角．

由，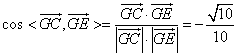

知二面角为．