练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设0＜θ＜,曲线x2sinθ+y2cosθ=1和x2cosθ-y2sinθ=1有4个不同的交点.

    (1)求θ的取值范围;

    (2)证明这4个交点共圆,并求圆半径的取值范围.

    思路解析：由经验知,要求θ的三角函数范围,想到两曲线有4个交点,则θ满足的方程组有4个解,问题(1)获解；要证四点共圆,由圆的定义可知,只需证明这4个点到某定点的距离相等即可.

    (1)解：设交点坐标为(x,y),

    则其满足方程组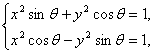即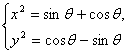有4个解,则x2＞0,y2＞0.

    ∴即

    又∵0＜θ＜,∴

    ∴θ的取值范围是(0,).

    (2)证明:由(1)得4个交点的坐标满足方程x2+y2=2cosθ(0＜θ＜),

    即=.

    ∴四个交点到原点的距离均等于.

    ∴四个交点共圆,半径r=.

    ∵0＜θ＜,∴＜r＜.∴圆半径的取值范围是(,).

    方法归纳

        解决多点共圆问题,只需证明这些点到某定点的距离均相等即可.定点是圆心,定距离是圆的半径.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设直线x+ky-1=0被圆O：x2+y2=2所截弦的中点的轨迹为M，则曲线M与直线x-y-1=0位置关系为（　　）
    A、相离B、相切C、相交D、不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点G是△ABC的重心，A（0，-1），B（0，1）．在x轴上有一点M，满足|
    MA
    |=|
    MC
    |    ，
    GM
    =λ
    AB
    (λ∈R)    （若△ABC的顶点坐标为A（x1，y1），B（x2，y2），C（x3，y3），则该三角形的重心坐标为G(
    x1+x2+x3
    3
    ，
    y1+y2+y3
    3
    )    ）．
    （1）求点C的轨迹E的方程．
    （2）设（1）中曲线E的左、右焦点分别为F1、F2，过点F2的直线l交曲线E于P、Q两点，求△F1PQ面积的最大值，并求出取最大值时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    m
    =(x2，y-cx)    ，
    n
    =(1，x+b)    ，
    m
    ∥
    n
    ，（x，y，b，c∈R），且把其中x，y所满足的关系式记为y=f（x），若f′（x）为f（x）的导函数，F（x）=f（x）+af′（x）（a＞0），且F（x）是R上的奇函数．
    （Ⅰ）求
    b
    a
    和c的值；
    （Ⅱ）若函数f（x）在[
    a
    2
    ，a2]    上单调递减，求b的取值范围；
    （Ⅲ）当a=2时，设0＜t＜4且t≠2，曲线y=f（x）在点A（t，f（t））处的切线与曲线y=f（x）相交于点B（m，f（m））（A，B不重合），直线x=t与y=f（m）相交于点C，△ABC的面积为S，试用t表示△ABC的面积S（t），若P为S（t）上一动点，D（4，0），求直线PD的斜率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•杭州模拟）如图，由半圆x2+y2=1（y≤0）和部分抛物线y=a（x2-1）（y≥0，a＞0）合成的曲线C称为“羽毛球形线”，且曲线C经过点（2，3）．
    （1）求a的值；
    （2）设A（1，0），B（-1，0），过A且斜率为k的直线l与“羽毛球形”相交于P，A，Q三点，问是否存在实数k使得∠QBA=∠PBA？若存在，求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设O为坐标原点,曲线x2+y2+2x-6y+1=0上有两点P、Q,满足关于直线x+my+4=0对称,又满足·=0.

    (1)求m的值;

    (2)求直线PQ的方程.

    查看答案和解析>>

    同步练习册答案