
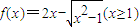
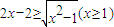 ,根据不等式的性质a≥b≥0?a2≥b2≥0,我们将不等式两边平方后即可将原不等式转化为整式不等式,进行即可求解.
,根据不等式的性质a≥b≥0?a2≥b2≥0,我们将不等式两边平方后即可将原不等式转化为整式不等式,进行即可求解.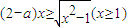 恒成立,由x≥1,我们易得2-a≤0,即a≥2时,不等式不可能恒成立,故我们仅须讨论2-a>0,即a≤2时的情况,即可得到答案.
恒成立,由x≥1,我们易得2-a≤0,即a≥2时,不等式不可能恒成立,故我们仅须讨论2-a>0,即a≤2时的情况,即可得到答案.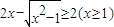
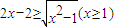
 }
}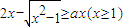 恒成立,
恒成立,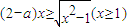 恒成立,
恒成立,

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:2010-2011学年河南省毕业班高三高考适应性考试数学理卷 题型:解答题
((本小题满分10分)选修4—5:不等式选讲
设函数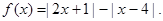
(I)解不等式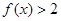 ;
;
(II)求函数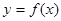 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com