
科目:高中数学 来源: 题型:
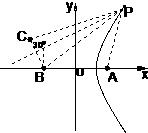 舰A在舰B的正东6千米处,舰C在舰B的北偏西30°且与B相距4千米,它们准备捕海洋动物,某时刻A发现动物信号,4秒后B、C同时发现这种信号,A发射麻醉炮弹 设舰与动物均为静止的,动物信号的传播速度为1千米/秒,若不计空气阻力与舰高,问舰A发射炮弹的方位角应是多少?
舰A在舰B的正东6千米处,舰C在舰B的北偏西30°且与B相距4千米,它们准备捕海洋动物,某时刻A发现动物信号,4秒后B、C同时发现这种信号,A发射麻醉炮弹 设舰与动物均为静止的,动物信号的传播速度为1千米/秒,若不计空气阻力与舰高,问舰A发射炮弹的方位角应是多少?查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省中原名校高三(上)期中数学试卷(文科)(解析版) 题型:选择题
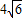
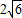
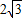
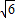
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com