求与圆C:(x-6)2+(y+2)2=1关于直4x-3y-5=0线对称的圆的方程.
【答案】
分析:依题意,求得圆C:(x-6)
2+(y+2)
2=1的圆心C(6,-2)关于直线4x-3y-5=0的对称点C′的坐标即可.利用线段CC′的中点M在直线4x-3y-5=0上,且直线CC′的斜率为-

即可求得M的坐标.
解答:解:设圆C:(x-6)
2+(y+2)
2=1的圆心C(6,-2)关于直线4x-3y-5=0的对称点为C′(x
,y
),CC′的中点为M,
依题意,点M在直线4x-3y-5=0上,且直线CC′的斜率为-

,
即
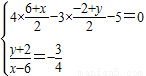
解得
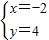
.
∴圆C:(x-6)
2+(y+2)
2=1关于直4x-3y-5=0线对称的圆的方程为:(x+2)
2+(y-4)
2=1.
点评:本题考查关于直线对称的圆的方程,求得圆C:(x-6)
2+(y+2)
2=1的圆心C(6,-2)关于直线4x-3y-5=0的对称点C′的坐标是关键,考查方程思想与转化思想的综合应用,属于中档题.

 即可求得M的坐标.
即可求得M的坐标. ,
,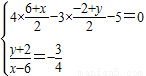 解得
解得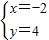 .
.
