分析:(Ⅰ)要证明:AB⊥AC1,只要证明AB垂直平面ACC1A1内的两条相交直线AC和A1A,即可证明AB⊥平面ACC1A1,从而证明AB⊥AC1.
(Ⅱ)设AC的中点为D,连接DN,A1D,只要证明A1D∥MN,即可证明MN∥平面ACC1A1;
(Ⅲ)法一:作出二面角M-AN-B的平面角,通过解三角形可求二面角M-AN-B的余弦值.
法二:建立空间直角坐标系,利用向量的数量积,求解二面角M-AN-B的余弦值.
解答:解法一:
(Ⅰ)证明:因为CC
1⊥平面ABC,
所以AC是AC
1在平面ABC内的射影,(2分)
由条件可知AB⊥AC,
所以AB⊥AC
1.(4分)
(Ⅱ)证明:设AC的中点为D,
连接DN,A
1D.
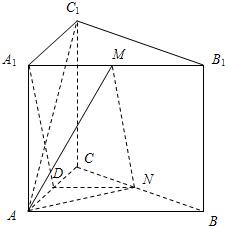
因为D,N分别是AC,BC的中点,
所以DN平行等于
AB.
又A
1M=
A
1B
1,A
1B
1平行等于AB,
所以A
1M平行等于DN.
所以四边形A
1DNM是平行四边形.
所以A
1D∥MN.(7分)
因为A
1D?平面ACC
1A
1,MN?平面ACC
1A
1,
所以MN∥平面ACC
1A
1.(9分)
(Ⅲ)如图,设AB的中点为H,连接MH,
所以MH∥BB
1.
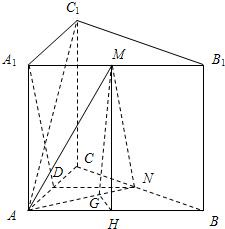
因为BB
1⊥底面ABC,
所以MH⊥底面ABC.
在平面ABC内,过点H做HG⊥AN,垂足为G.
连接MG,则MG⊥AN.
所以∠MGH是二面角M-AN-B的平面角.(12分)
因为MH=BB
1=2,
由△AGH∽△BAC,得HG=
.
所以MG=
=
.
所以cos∠MGH=
=
.
二面角M-AN-B的余弦值是
.(14分)
解法二:
依条件可知AB,AC,AA
1两两垂直.
如图,以点A为原点建立空间直角坐标系A-xyz.
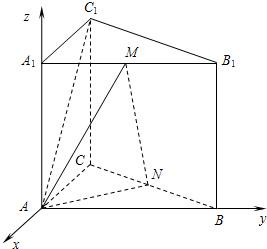
根据条件容易求出如下各点坐标:
A(0,0,0),B(0,2,0),C(-1,0,0),A
1(0,0,2),B
1(0,2,2),C
1(-1,0,2),M(0,1,2),
N(-,1,0).
证明:(Ⅰ):因为
=(0,2,0),
=(-1,0,2),
所以
•=0×(-1)+2×0+0×2=0.(2分)
所以
⊥.
即AB⊥AC
1.(4分)
(Ⅱ)证明:因为
=(-,0,-2),
=(0,2,0)是平面ACC
1A
1的一个法向量,
且
•=
-×0+0×2-2×0=0,所以
⊥.(7分)
又MN?平面ACC
1A
1,
所以MN∥平面ACC
1A
1.(9分)
(Ⅲ)设n=(x,y,z)是平面AMN的法向量,
因为
=(0,1,2),
=(-,1,0),
由
得
解得平面AMN的一个法向量n=(4,2,-1).
由已知,平面ABC的一个法向量为m=(0,0,-1).(12分)
设二面角M-AN-B的大小为θ,则
cosθ==
=
.
二面角M-AN-B的余弦值是
.(14分)
点评:本题考查直线与直线的垂直,直线与平面的平行,二面角的知识,考查学生的空间想象能力,逻辑思维能力,是中档题.

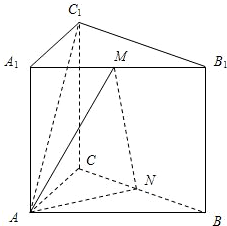 已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.
已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.




 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案