
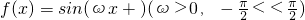 ,给出以下四个论断:
,给出以下四个论断: 对称;
对称; ,0)对称;
,0)对称;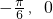 ]上是增函数.
]上是增函数. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2007届深圳市龙华中英文实验学校理科数学测试题 题型:022
设函数![]() ,给出以下四个论断:①
,给出以下四个论断:①![]() 的周期为π;②
的周期为π;②![]() 在区间(-
在区间(-![]() ,0)上是增函数;?③
,0)上是增函数;?③![]() 的图象关于点(
的图象关于点(![]() ,0)对称;?④
,0)对称;?④![]() 的图象关于直线
的图象关于直线![]() 对称.?以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:?________
对称.?以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:?________![]() ________(只需将命题的序号填在横线上).
________(只需将命题的序号填在横线上).
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省梅州市高一(上)第二次质检数学试卷(解析版) 题型:填空题
 ,给出以下四个论断:
,给出以下四个论断: 对称;
对称;  对称;
对称;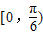 上是增函数.
上是增函数.查看答案和解析>>
科目:高中数学 来源:2011年江苏省高一上学期期末考试数学试卷 题型:填空题
设函数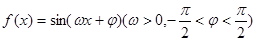 ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线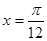 对称; ③它的最小正周期是
对称; ③它的最小正周期是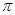 ;
;
②它的图象关于点( ,0)对称;④在区间[
,0)对称;④在区间[ ]上是增函数.
]上是增函数.
以其中两个论断作为条件,余下论断作为结论,写出一个正确的命题:
条件_ ▲ _ ,结论_▲ (填序号)
查看答案和解析>>
科目:高中数学 来源:2014届江苏省高一12月月考数学试卷 题型:填空题
设函数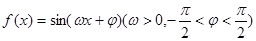 ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线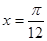 对称; ③它的最小正周期是
对称; ③它的最小正周期是 ;
;
②它的图象关于点(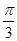 ,0)对称;
④在区间[
,0)对称;
④在区间[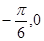 ]上是增函数.
]上是增函数.
以其中两个论断作为条件,余下论断作为结论,写出一个正确的命题:
条件_ ▲ _ ,结论_ ▲ (填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数![]() ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线![]() 对称; ③它的最小正周期是
对称; ③它的最小正周期是![]() ;
;
②它的图象关于点(![]() ,0)对称;④在区间[
,0)对称;④在区间[![]() ]上是增函数.
]上是增函数.
以其中两个论断作为条件,余下论断作为结论,写出一个正确的命题:
条件_ ▲ _ ,结论_▲ (填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com