
已知函数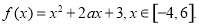
(1)当 =-2时,求
=-2时,求 的最值;
的最值;
(2)求实数 的取值范围,使
的取值范围,使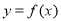 在区间
在区间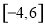 上是单调函数.
上是单调函数.
(1) ,
, ;(2)
;(2) .
.
【解析】
试题分析:(1)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动,不论哪种类型,解题的关键是对称轴与区间的关系,当含有参数时,要依据对称轴与区间的关系进行分类讨论;(2)二次函数、二次方程与二次不等式统称“三个”二次,它们常结合在一起,有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法,一般从:①开口方向;②对称轴位置;③判别式;④端点值符合四个方面分析;(3)二次函数的综合问题应用多涉及单调性与最值或二次方程根的分布问题,解决的主要思路是等价转化,多用到数形结合思想与分类讨论思想,
试题解析:解(1)当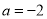 时,
时,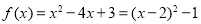 ,
,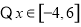 对称轴为
对称轴为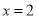
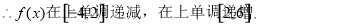
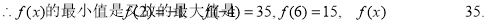
(2)要使函数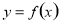 在区间
在区间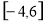 上是单调函数,则对称轴
上是单调函数,则对称轴 ,
,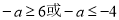 ,解之得,
,解之得,
考点:一元二次函数在闭区间上的最值;(2)一元二次函数的单调性.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:2016届黑龙江省高一下学期期中数学试卷(解析版) 题型:解答题
数列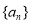 的前
的前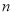 项和为
项和为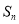 ,
,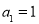 ,
,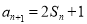 ,等差数列
,等差数列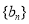 满足
满足 ,
,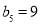 .
.
(1)求数列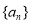 ,数列
,数列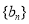 的通项公式;
的通项公式;
(2)若对任意的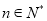 ,不等式
,不等式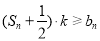 恒成立,求实数
恒成立,求实数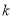 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届黑龙江省高一下学期期末考试数学试卷(解析版) 题型:选择题
已知直线y=kx与圆x2+y2=3相交于M,N两点,则|MN|等于( )
A.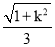 B.
B.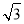 C.
C. D.2
D.2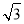
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com