练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．在△ABC中，BD：DC=2：1，AE：EC=1：3，求OB：OE．

    分析 根据梅涅劳斯定理得出：$\frac{BO}{OE}$=$\frac{BD}{DC}$•$\frac{CA}{AE}$，再根据题意求得$\frac{BD}{DC}$和$\frac{CA}{AE}$的值，代入即可解出结果．

    解答 解：梅涅劳斯定理，
    $\frac{BO}{OE}$=$\frac{BD}{DC}$•$\frac{CA}{AE}$，
    因为BD：DC=2：1，所以$\frac{BD}{DC}$=2，
    又因为AE：EC=1：3，所以$\frac{CA}{AE}$=4，
    所以，$\frac{BO}{OE}$=2×4=8，
    即OB：OE=8：1．

    点评 本题主要考查了运用梅涅劳斯定理解决平面几何问题，主要是解决线段长度的比例问题，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

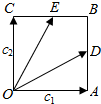    18．如图所示，四边形OABC是边长为1的正方形，$\overrightarrow{OA}$=e1，$\overrightarrow{OC}$=e2，D、E分别为AB、BC中点．
    求：①用e1、e2表示$\overrightarrow{OD}$，$\overrightarrow{OE}$；
    ②计算$\overrightarrow{OD}$•$\overrightarrow{OE}$；
    ③∠DOE=θ，求cosθ

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．{（x，y）|xy＞0}表示位于第一、三象限的点的集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若a、b、c、d∈R+，且a+b=8，c+d=12，则|（a+bi）（c+di）|的最小值是（　　）
    A．24B．36C．48D．60

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知a+b+c=0，求证：a3+a2c+b2c-abc+b3=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．如图1所示：在边长为12的正方形AA′A${\;}_{1}^{′}$A1中，BB1∥CC1∥AA1，且AB=3，BC=4，AA${\;}_{1}^{′}$分别交BB1、CC1于P，Q两点，将正方形沿BB1、CC1折叠，使得A′A${\;}_{1}^{′}$与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1．
    （Ⅰ）在底边AC上有一点M，且AM：MC=3：4，求证：BM∥平面APQ；
    （Ⅱ）求直线BC与平面A1PQ所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．如图所示，在侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中，AD∥BC，AD⊥AB，AB═$\sqrt{2}$，AD=2，BC=4，AA1=2，E，F分别是DD1，AA1的中点．
    （I）证明：EF∥平面B1C1CB；
    （Ⅱ）求BC1与平面B1C1F所成的角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在直角坐标系xoy中，曲线C1：$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$（t为参数，t≠0），其中0≤α＜π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，曲线C3：ρ=2$\sqrt{3}$cosθ．
    （I）．求C2与C1交点的直角坐标；
    （Ⅱ）若C2与C1相交于点A，C3与C1相交于点B，求|AB|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．一个正方体的平面展开图及该正方体的直观图的示意图如图所示．
    （1）判断平面BEG与平面ACH的位置关系．并证明你的结论；
    （2）若正方体棱长为1，求三棱锥F-BEG的体积．

    查看答案和解析>>

    同步练习册答案