练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

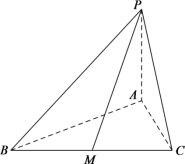
    【题目】在三棱锥中，底面是边长为6的正三角形，底面，且与底面所成的角为．

    （1）求三棱锥的体积；

    （2）若是的中点，求异面直线与所成角的大小（结果用反三角函数值表示）.

    【答案】（1）（2）

    【解析】

    （1）由底面,可得为与平面所成的角,且,因此在中,,则,代入求值即可；

    （2）设为棱的中点,连接,可得,则与的夹角为异面直线与所成的角,即为,由和求得,在利用余弦定理即可求出

    解：（1）因为平面,所以为与平面所成的角,

    由与平面所成的角为,可得,

    因为平面,平面,所以,

    又,可知,

    所以

    （2）设为棱的中点,连接,

    由分别是棱的中点,可得,

    所以与的夹角为异面直线与所成的角,即为,

    因为平面,平面,所以,,

    又,,,

    所以,

    ,

    所以,

    故异面直线与所成的角为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）

    A. 1盏 B. 3盏 C. 5盏 D. 9盏

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果存在常数a，使得数列{an}满足：若x是数列{an}中的一项，则a-x也是数列{an}中的一项，称数列{an}为“兑换数列”，常数a是它的“兑换系数”．

    （1）若数列：2，3，6，m（m＞6）是“兑换系数”为a的“兑换数列”，求m和a的值；

    （2）已知有穷等差数列{bn}的项数是n0（n0≥3），所有项之和是B，求证：数列{bn}是“兑换数列”，并用n0和B表示它的“兑换系数”；

    （3）对于一个不少于3项，且各项皆为正整数的递增数列{cn}，是否有可能它既是等比数列，又是“兑换数列”？给出你的结论，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年双十一落下帷幕,天猫交易额定格在268(单位:十亿元)人民币(下同),再创新高,比去年218(十亿元)多了50(十亿元),这些数字的背后,除了是消费者买买买的表现,更是购物车里中国新消费的奇迹,为了研究历年销售额的变化趋势,一机构统计了2010年到2019年天猫双十一的销售额数据(单位:十亿元).绘制如下表1:

    表1

    年份

    2010

    2011

    2012

    2013

    2014

    2015

    2016

    2017

    2018

    2019

    编号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    销售额

    0.9

    8.7

    22.4

    41

    65

    94

    132.5

    172.5

    218

    268

    根据以上数据绘制散点图,如图所示.

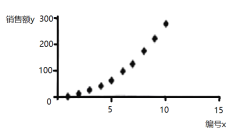
    (1)根据散点图判断,与哪一个适宜作为销售额关于的回归方程类型？(给出判断即可,不必说明理由)

    (2)根据(1)的判断结果及下表中的数据,建立关于的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)

    (3)把销售额超过10(十亿元)的年份叫“畅销年”,把销售额超过100(十亿元)的年份叫“狂欢年”,从2010年到2019年这十年的“畅销年”中任取3个,求取到的“狂欢年”个数的分布列与期望.

    参考数据:.

    参考公式:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计公式分别为,.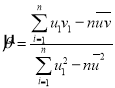

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    (1)讨论函数的单调性;

    (2)设,当函数与的图象有三个不同的交点时,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】气象意义上从春季进入夏季的标志为连续5天的日平均温度均不低于22℃.现有甲、乙、丙三地连续5天的日平均温度的记录数据：（记录数据都是正整数）

    ①甲地5个数据的中位数为24，众数为22；

    ②乙地5个数据的中位数为27，总体均值为24；

    ③丙地5个数据中有一个数据是32，总体均值为26，总体方差为10.8.

    则肯定进入夏季的地区有_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

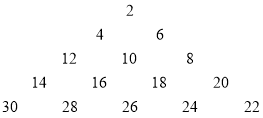
    【题目】已知从2开始的连续偶数蛇形排列形成宝塔形数表，第一行为2，第一行为46，第三行为12，10，8，第四行为14，16，18，20.如图所示，在宝塔形数表中位于第i行，第j列的数记为，比如，，，，若，则（ ）

    A.65B.70C.71D.72

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱锥中，平面平面，，，点，分别是棱，的中点，点是的重心.

    （1）证明：平面；

    （2）若与平面所成的角为，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展，下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表：

    年份

    2014

    2015

    2016

    2017

    2018

    销量（万台）

    8

    10

    13

    25

    24

    某机构调查了该地区30位购车车主的性别与购车种类情况，得到的部分数据如下表所示：

    购置传统燃油车

    购置新能源车

    总计

    男性车主

    6

    24

    女性车主

    2

    总计

    30

    （1）求新能源乘用车的销量关于年份的线性相关系数，并判断与是否线性相关；

    （2）请将上述列联表补充完整，并判断是否有的把握认为购车车主是否购置新能源乘用车与性别有关；

    参考公式：，，其中.，若，则可判断与线性相关.

    附表：

    0．10

    0.05

    0.025

    0.010

    0.001

    2.706

    3.841

    5.024

    6.635

    10.828

    查看答案和解析>>

    同步练习册答案