
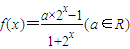 .
.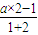 =0,解可得a的值,
=0,解可得a的值, ,解可得h、k的值,即可得f(x)的对称性与其对称中心的坐标.
,解可得h、k的值,即可得f(x)的对称性与其对称中心的坐标.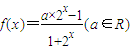 ,有1+2x>1恒成立,
,有1+2x>1恒成立,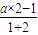 =0,解可得a=1,
=0,解可得a=1,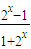 ;
; =5-
=5- ,
,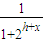 +
+ )=2k恒成立,
)=2k恒成立,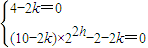 ,解可得h=0,k=2,
,解可得h=0,k=2,

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:宁夏回族自治区月考题 题型:解答题
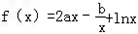 .
. 处取和极值,
处取和极值,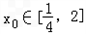 ,使得不等式f(
,使得不等式f(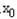 )-c≤0成立,求c的最小值;
)-c≤0成立,求c的最小值;查看答案和解析>>
科目:高中数学 来源:2013年广东省汕头市高考数学一模试卷(理科)(解析版) 题型:解答题
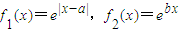 .
.查看答案和解析>>
科目:高中数学 来源:2010年高考数学预测试卷(押题卷1)(解析版) 题型:解答题
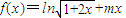 .
.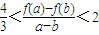 .
.查看答案和解析>>
科目:高中数学 来源:2010年四川省攀枝花市高考数学三模试卷(理科)(解析版) 题型:解答题
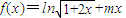 .
.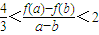 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com