
![]() 个排成一排,在下列情况下,各有多少种不同排法?
个排成一排,在下列情况下,各有多少种不同排法?
(1)甲排头,
(2)甲不排头,也不排尾,
(3)甲、乙、丙三人必须在一起,
(4)甲、乙之间有且只有两人,
(5)甲、乙、丙三人两两不相邻,
(6)甲在乙的左边(不一定相邻),
(7)甲、乙、丙三人按从高到矮,自左向右的顺序,
(8)甲不排头,乙不排当中。解析:(1)甲固定不动,其余有![]() ,即共有
,即共有![]() 种;
种;
(2)甲有中间![]() 个位置供选择,有
个位置供选择,有![]() ,其余有
,其余有![]() ,即共有
,即共有![]() 种;
种;
(3)先排甲、乙、丙三人,有![]() ,再把该三人当成一个整体,再加上另四人,相当于
,再把该三人当成一个整体,再加上另四人,相当于![]() 人的全排列,即
人的全排列,即![]() ,则共有
,则共有![]() 种;
种;
(4)从甲、乙之外的![]() 人中选
人中选![]() 个人排甲、乙之间,有
个人排甲、乙之间,有![]() ,甲、乙可以交换有
,甲、乙可以交换有![]() ,
,
把该四人当成一个整体,再加上另三人,相当于![]() 人的全排列,
人的全排列,
则共有![]() 种;
种;
(5)先排甲、乙、丙之外的四人,有![]() ,四人形成五个空位,甲、乙、丙三人排
,四人形成五个空位,甲、乙、丙三人排
这五个空位,有![]() ,则共有
,则共有![]() 种;
种;
(6)不考虑限制条件有![]() ,甲在乙的左边(不一定相邻),占总数的一半,
,甲在乙的左边(不一定相邻),占总数的一半,
即![]() 种;
种;
(7)先在![]() 个位置上排甲、乙、丙之外的四人,有
个位置上排甲、乙、丙之外的四人,有![]() ,留下三个空位,甲、乙、丙三人按从高到矮,自左向右的顺序自动入列,不能乱排的,即
,留下三个空位,甲、乙、丙三人按从高到矮,自左向右的顺序自动入列,不能乱排的,即![]()
(8)不考虑限制条件有![]() ,而甲排头有
,而甲排头有![]() ,乙排当中有
,乙排当中有![]() ,这样重复了甲排头,乙排当中
,这样重复了甲排头,乙排当中![]() 一次,即
一次,即![]()


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源:2014届吉林省吉林市高二3月月考理科数学试卷(解析版) 题型:解答题
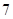 个排成一排,在下列情况下,各有多少种不同排法?
个排成一排,在下列情况下,各有多少种不同排法?
(1)甲排头,(2)甲不排头,也不排尾,(3)甲、乙、丙三人必须在一起,
(4)甲、乙之间有且只有两人,(5)甲、乙、丙三人两两不相邻。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com