
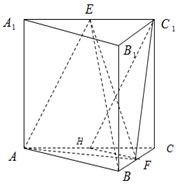
 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.分析 (1)证明HF∥AB.EC1∥AH,推出C1H∥AE,然后证明平面C1HF∥平面ABE.
(2)证明AF⊥BC,B1B⊥AF,得到AF⊥平面B1BCC1,然后证明平面AEF⊥平面B1BCC1
解答 (本小题8分)证明:(1)∵F,H分别是BC,AC的中点,∴HF∥AB.
又∵E,H分别是A1C1,AC的中点,∴EC1∥AH
又∵EC1=AH∴四边形EC1HA为平行四边形.∴C1H∥AE,
又∵C1H∩HF=H,AE∩AB=A,
所以平面C1HF∥平面ABE.
(2)∵AB=AC,F为BC中点,∴AF⊥BC,∵B1B⊥平面ABC,AF?平面ABC,
∴B1B⊥AF,∵B1B∩BC=B,∴AF⊥平面B1BCC1
又∵AF?平面AEF,
∴平面AEF⊥平面B1BCC1
点评 本题考查平面与平面垂直以及平面与平面平行的判定定理的应用,考查空间想象能力以及逻辑推理能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | π-3 | C. | 3-$\frac{π}{2}$ | D. | $\frac{π}{2}$-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
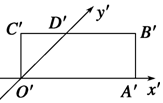 如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )
如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )| A. | 正方形 | B. | 矩形 | C. | 梯形 | D. | 菱形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com