
已知二次函数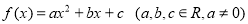 ,
,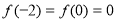 ,
,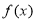 的最小值为
的最小值为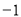 .
.
⑴求函数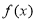 的解析式;
的解析式;
⑵设 ,若
,若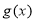 在
在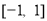 上是减函数,求实数
上是减函数,求实数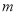 的取值范围;
的取值范围;
⑶设函数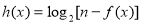 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数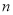 的取值范围.[
的取值范围.[
(1)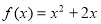 ;(2)
;(2)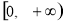 ;(3)
;(3)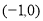 。
。
【解析】
试题分析:(1)由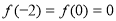 可设
可设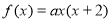 ,再由
,再由 的最小值
的最小值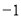 求a的值;(2)首先对
求a的值;(2)首先对
二次项系数分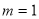 、
、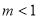 、
、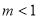 三种情况讨论,然后确定对称轴
三种情况讨论,然后确定对称轴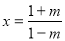 与给定区间
与给定区间
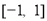 端点的关系;(3)要满足题意,须有
端点的关系;(3)要满足题意,须有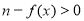 有解,且
有解,且 无解.然后求
无解.然后求
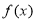 的最小值,令
的最小值,令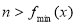 ,但
,但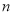 不属于
不属于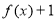 的值域,即可得实数
的值域,即可得实数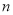 的取值范围。
的取值范围。
⑴ 由题意设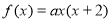 ,
,
∵ 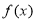 的最小值为
的最小值为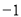 , ∴
, ∴ 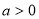 ,且
,且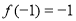 , ∴
, ∴ 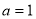 ,
,
∴ 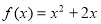 .
.
⑵ ∵ 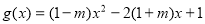 ,
,
①当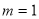 时,
时,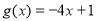 在[?1, 1]上是减函数,∴
在[?1, 1]上是减函数,∴ 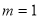 符合题意.
符合题意.
② 当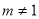 时,对称轴方程为:
时,对称轴方程为: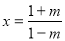 ,
,
ⅰ)当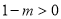 ,即
,即 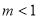 时,抛物线开口向上,
时,抛物线开口向上,
由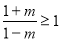 , 得
, 得 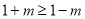 , ∴
, ∴  ;
;
ⅱ)当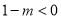 , 即
, 即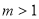 时,抛物线开口向下,
时,抛物线开口向下,
由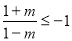 ,得
,得 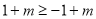 , ∴
, ∴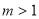 .
.
综上知,实数 的取值范围为
的取值范围为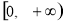 .
.
⑶法一:∵ 函数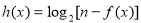 在定义域内不存在零点,必须且只须有
在定义域内不存在零点,必须且只须有
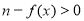 有解,且
有解,且 无解.
无解.
∴ 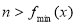 ,且
,且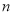 不属于
不属于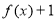 的值域,
的值域,
又∵ 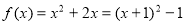 ,
,
∴ 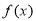 的最小值为
的最小值为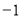 ,
,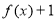 的值域为
的值域为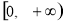 ,
,
∴  ,且
,且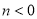
∴ 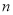 的取值范围为
的取值范围为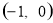 .
.
法二: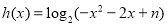 ,令
,令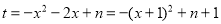 ,
,
必有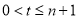 ,得
,得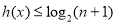 ,
,
因为函数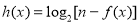 在定义域内不存在零点,
在定义域内不存在零点,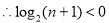 ,
,
得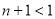 ,即
,即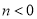 ,又
,又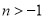 (否则函数定义域为空集,不是函数),
(否则函数定义域为空集,不是函数),
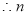 的取值范围是
的取值范围是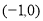 。
。
考点:(1)待定系数法求函数的解析式;(2)二次项系数及二次函数对称轴与给定区间引起的分类讨论;(3)构造函数研究函数的零点个数。


科目:高中数学 来源:2016届山东省高一下学期期中考试数学试卷(解析版) 题型:填空题
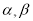 是两个不同的平面,
是两个不同的平面, 是平面
是平面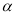 及
及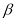 之外的两条不同直线,给出四个论断:
之外的两条不同直线,给出四个论断:
①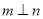 ②
②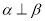 ③
③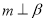 ④
④ 。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
查看答案和解析>>
科目:高中数学 来源:2016届山东省济宁市高一二月检测数学试卷(解析版) 题型:选择题
将函数f(x)=sinωx(其中ω>0)的图象向右平移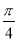 个单位长度,所得图象经过点(
个单位长度,所得图象经过点(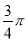 ,0),则ω的最小值是( )
,0),则ω的最小值是( )
A.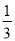 B.1 C.
B.1 C.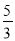 D.2
D.2
查看答案和解析>>
科目:高中数学 来源:2016届山东省济宁市高一二月检测数学试卷(解析版) 题型:选择题
已知函数y=sin(ωx+φ)(ω>0,|φ|<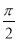 )的部分图象如图所示,则( )
)的部分图象如图所示,则( )

A.ω=2,φ=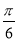 B.ω=1,φ=-
B.ω=1,φ=-
C.ω=1,φ= D.ω=2,φ=-
D.ω=2,φ=-
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com