
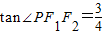 ,则椭圆的离心率为 .
,则椭圆的离心率为 . 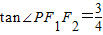 ,可得PF2=
,可得PF2= c,再由勾股定理算出PF1=
c,再由勾股定理算出PF1= c,根据椭圆的定义得2a=PF1+PF2=4c,最后根据离心率的计算公式,可以算出该椭圆的离心率.
c,根据椭圆的定义得2a=PF1+PF2=4c,最后根据离心率的计算公式,可以算出该椭圆的离心率.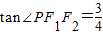 ,
,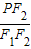 =
= ,结合F1F2=2c为焦距,可得PF2=
,结合F1F2=2c为焦距,可得PF2= c
c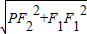 =
= c
c c+
c+ c=4c
c=4c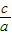 =
=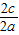 =
=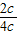 =
=



 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com