
| 7 |
| 3 |
A、(-
| ||||||
B、(-
| ||||||
C、(-
| ||||||
D、(-
|
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知圆柱OO1底面半径为1,高为π,ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线Γ如图所示.将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1与曲线Γ相交于点P.
已知圆柱OO1底面半径为1,高为π,ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线Γ如图所示.将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1与曲线Γ相交于点P.| π |
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:湖南省期中题 题型:解答题
抛物线C的顶点在坐标原点,焦点在y轴的负半轴上,过点M(0,-2)作直线l与抛物线C交于A,B两点,且满足 =(-4,-12)。
=(-4,-12)。
(1)求直线l和抛物线C的方程;
(2)当抛物线C上一动点P从点A向点B运动时,求△ABP的面积的最大值;
(3)在抛物线C上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉六中高三(上)12月月考数学试卷(理科)(解析版) 题型:解答题
 时,求点C1到平面APB的距离;
时,求点C1到平面APB的距离; ?若存在,求出线段BP的长度;若不存在,请说明理由.
?若存在,求出线段BP的长度;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉六中高三(上)12月月考数学试卷(理科)(解析版) 题型:解答题
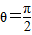 时,求点C1到平面APB的距离;
时,求点C1到平面APB的距离;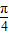 ?若存在,求出线段BP的长度;若不存在,请说明理由.
?若存在,求出线段BP的长度;若不存在,请说明理由.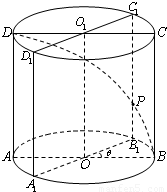
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com