抛物线y2=4x焦点F,则经过点F,M(4,4)且与抛物线的准线相切的圆的个数为________.
2
分析:根据抛物线的方程求得焦点坐标和准线的方程,设出所求圆的圆心,表示出半径,则圆的方程可得,把M,F点的坐标代入整理求得h,和g,则圆的方程可求.
解答:解:抛物线y
2=4x的焦参数p=2,所以F(1,0),准线l:x=-1,即x+1=0,
设经过点M(4,4)、F(1,0),且与直线l相切的圆的圆心为Q(a,b),
则半径为Q到l的距离为即1+a,
∴所以圆的方程为(x-a)
2+(y-b)
2=(1+a)
2;
将M、F的坐标代入,(4-a)
2+(4-b)
2=(1+a)
2①,
(1-a)
2+b
2=(1+a)
2②,
由①②得:b
2-8b+1=10a,③
b
2=4a,④
由③④得:3b
2+16b-2=0,
解得b
1=
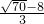
,b
2=
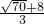
.
将b
1,b
2分别代入④得:a
1=
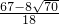
,a
2=
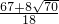
.
故圆的个数为2个.
故答案为:2.
点评:本题主要考查了抛物线的简单性质和圆的标准方程.考查了运用待定系数法求圆的方程以及圆与圆锥曲线的位置关系,考查运算能力,属于难题.

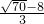 ,b2=
,b2=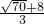 .
.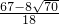 ,a2=
,a2=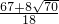 .
.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案