
| A. |  | B. |  | C. |  | D. |  |
分析 推导出g(x)=-logbx=log$\frac{1}{b}$x,$\frac{1}{b}$=a,由此利用指数函数、对数函数的图象和性质能求出结果.
解答 解:g(x)=-logbx=log$\frac{1}{b}$x,
∵a>0,b>0且ab=1,
∴当a>1时,$\frac{1}{b}$=a>1,此时函数f(x)=ax的图象过点(0,1),图象在x轴上方,是增函数,
g(x)=-logbx的图象过点(1,0),图象在y轴左侧,是增函数,B满足条件;
当0<a<1时,$\frac{1}{b}$=a∈(0,1),此时函数f(x)=ax的图象过点(0,1),图象在x轴上方,是增减数,
g(x)=-logbx的图象过点(1,0),图象在y轴左侧,是减函数,都不满足条件.
故选:B.
点评 本题考查指数函数与对数函数的图象,以及函数图象的平移变换,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $?x∈R,\root{3}{x}+1>0$ | |
| B. | 小概率事件就是不可能发生的事件,大概率事件就是必然要发生的事件 | |
| C. | p∨q为真命题,则命题p与q均为真命题 | |
| D. | 命题“$?{x_0}∈R,{x_0}^2-{x_0}>0$的命题的否定是“?x∈R,x2-x≤0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1+a8=a4+a5 | B. | a1+a8<a4+a5 | ||
| C. | a1+a8>a4+a5 | D. | a1+a8与a4+a5大小关系不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
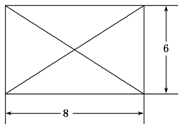 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
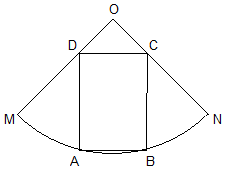 如图,有一块扇形草地OMN,已知半径为R,∠MON=$\frac{π}{2}$,现要在其中圈出一块矩形场地ABCD作为儿童乐园使用,其中点A、B在弧MN上,且线段AB平行于线段MN
如图,有一块扇形草地OMN,已知半径为R,∠MON=$\frac{π}{2}$,现要在其中圈出一块矩形场地ABCD作为儿童乐园使用,其中点A、B在弧MN上,且线段AB平行于线段MN查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com