练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    椭圆是描述天体运行轨迹时常用的曲线，也是日常生活中常见的曲线．椭圆的光学性质在现实生活中应用十分广泛，如从椭圆的一个焦点处发出的光线射到椭圆上，经反射后通过另外一个焦点．电影放映机上的聚光灯泡的反射镜轴截面是椭圆的一部分（如图 所示）．灯丝在焦点F2处，而且灯丝与反射镜的顶点A的距离|F2A|=1.5 cm，椭圆的通径|BC|=5.4 cm．为了使电影放映机，灯泡应安在距片门多远的地方？
    解：设焦距|F1F2|=2c ．|OA|=a ，由题设可知B 点的坐标为(c，2.7) ，
    根据椭圆的定义得|BF1|+|BF2|=2a=2|OA|,
    即+2.7=2(c+1.5)，解得2c= 12.
    ∴灯泡应安在距片门12cm的地方．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

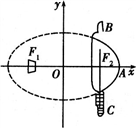
    精英家教网学校科技小组在计算机上模拟航天器变轨返回试验．设计方案如图：航天器运行（按顺时针方向）的轨迹方程为
    x2
    100
    +
    y2
    25
    =1    ，变轨（即航天器运行轨迹由椭圆变为抛物线）后返回的轨迹是以y轴为对称轴、M(0，
    64
    7
    )    为顶点的抛物线的实线部分，降落点为D（8，0）．观测点A（4，0）、B（6，0）同时跟踪航天器．
    （1）求航天器变轨后的运行轨迹所在的曲线方程；
    （2）试问：当航天器在x轴上方时，观测点A、B测得离航天器的距离分别为多少时，应向航天器发出变轨指令？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

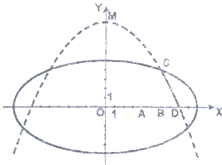    （2006•蚌埠二模）“神六”上天并顺利返回，让越来越多的青少年对航天技术发生了兴趣．某学校科技小组在计算机上模拟航天器变轨返回试验，设计方案
    如图：航天器运行（按顺时针方向）的轨迹方程为
    x2
    100
    +
    y2
    25
    =1，变轨（航天器运行轨迹由椭圆变为抛物线）后返回的轨迹是以y轴为
    对称轴、M（0，
    64
    7
    ）为顶点的抛物线的实线部分，降落点为D（8，0），观测点A（4，0）、B（6，0）同时跟踪航天器．试问：当航天器在x轴上方时，观测点A、B测得离航天器的距离分别为
    2
    		5
    、4
    2
    		5
    、4
    时航天器发出变轨指令．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如下图:航天器运行(按顺时针方向)的轨迹方程为,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴,M(0,)为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0),B(6,0)同时跟踪航天器.

    (1)求航天器变轨后的运行轨迹所在的曲线方程;

    (2)试问:当航天器在x轴上方时,观测点A,B测得离航天器的距离分别为多少时,应向航天器发出变轨指令?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图：航天器运行（按顺时针方向）的轨迹方程为，变轨（即航天器运行轨迹由椭圆变为抛物线）后返回的轨迹是以轴为对称轴、 为顶点的抛物线的实线部分，降落点为. 观测点同时跟踪航天器. 试问：当航天器在轴上方时，观测点测得离航天器的距离分别为多少时，应向航天器发出变轨指令？

    查看答案和解析>>

    同步练习册答案