
如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
(1)求四棱锥P-ABCD的体积;
(2)证明:BD∥平面PEC;
(3)若G为BC上的动点,求证:AE⊥PG.
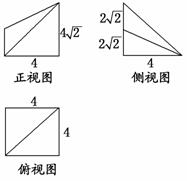
解:(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,且PA=4![]() ,BE=2
,BE=2![]() ,AB=AD=CD=CB=4,
,AB=AD=CD=CB=4,
∴VP-ABCD=![]() PA×SABCD=
PA×SABCD=![]() ×4
×4![]() ×4×4=
×4×4=![]() .
.
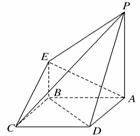
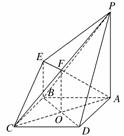
(2)证明:连结AC交BD于O点,
取PC中点F,连结OF,
 |
∵EB∥PA,且EB=![]() PA,
PA,
又OF∥PA,且OF=![]() PA,
PA,
∴EB∥OF,且EB=OF,∴四边形EBOF为平行四边形,∴EF∥BD.
又EF⊂平面PEC,BD⊄平面PEC,所以BD∥平面PEC.
(3)连结BP,∵![]() =
=![]() =
=![]() ,∠EBA=∠BAP=90°,
,∠EBA=∠BAP=90°,
∴△EBA∽△BAP,∴∠PBA=∠BEA,∴∠PBA+∠BAE=∠BEA+∠BAE=90°,∴PB⊥AE.
又∵BC⊥平面APEB,∴BC⊥AE,∴AE⊥平面PBG,∴AE⊥PG.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
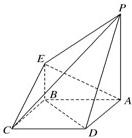 如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).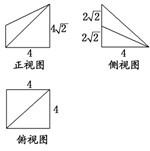
查看答案和解析>>
科目:高中数学 来源: 题型:
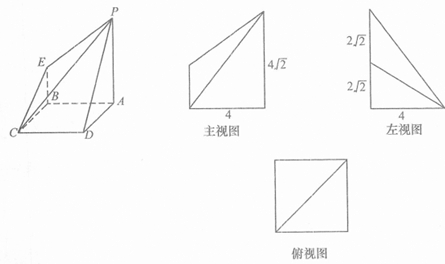
查看答案和解析>>
科目:高中数学 来源: 题型:
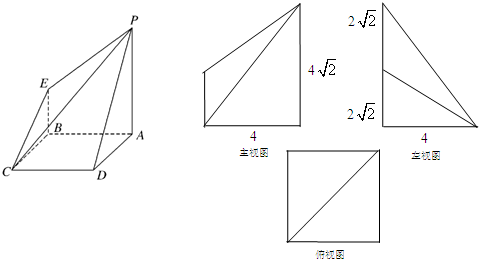
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com