
 已知函数
已知函数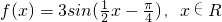 .
. 解:(1)函数f(x)的周期
解:(1)函数f(x)的周期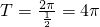 ,
,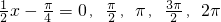 ,解得
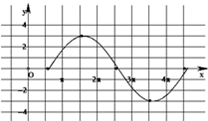
,解得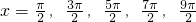 .列表如下:
.列表如下:| x |  |  |  | 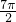 |  |
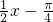 | 0 |  | π |  | 2π |
3sin(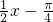 ) ) | 0 | 3 | 0 | -3 | 0 |
 个单位,然后把所有点的横坐标扩大为原来的2倍,再把所有点的纵坐标扩大为原来的3倍,得到f(x)的图象.…(8分)
个单位,然后把所有点的横坐标扩大为原来的2倍,再把所有点的纵坐标扩大为原来的3倍,得到f(x)的图象.…(8分) 个单位,得到f(x)的图象.…(8分)
个单位,得到f(x)的图象.…(8分)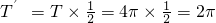 …(9分)
…(9分)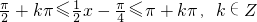 ,…(10分) 得
,…(10分) 得 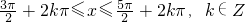 ,
,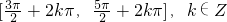 .…(12分)
.…(12分) 个单位,然后把所有点的横坐标扩大为原来的2倍,再把所有点的纵坐标扩大为原来的3倍,得到f(x)的图象.
个单位,然后把所有点的横坐标扩大为原来的2倍,再把所有点的纵坐标扩大为原来的3倍,得到f(x)的图象. 个单位,得到f(x)的图象.
个单位,得到f(x)的图象.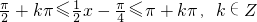 ,
,

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源:2009-2010学年高一(下)模块考试数学试卷(必修4)(解析版) 题型:解答题
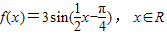 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测(一)理数学卷(解析版) 题型:解答题
已知函数 .
.
(1)画出函数 的图象,写出函数
的图象,写出函数 的单调区间;
的单调区间;
(2)解关于 的不等式
的不等式
 .
.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高一上学期10月月考数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数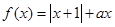 (
(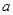 ∈R).
∈R).
(1)画出当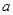 =2时的函数
=2时的函数 的图象;
的图象;
(2)若函数 在R上具有单调性,求
在R上具有单调性,求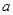 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013届新疆喀什二中高二下期中文科数学(1、3、4部)(解析版) 题型:解答题
(本小题满分12分)已知函数 ,
,
(1)画出函数 图像;
图像;
(2)求 的值;
的值;
(3)当 时,求
时,求 取值的集合.
取值的集合.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com