
| 1 |
| 2 |
| a+b |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a+b |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源:2012-2013学年江苏省盐城市大丰市新丰中学高三(上)期中数学试卷(文科)(解析版) 题型:填空题
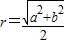 ”.对于“若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c”,类比上述处理方法,可得该三棱锥的外接球半径为R= .
”.对于“若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c”,类比上述处理方法,可得该三棱锥的外接球半径为R= .查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市淮阴中学高三(上)第四次调研数学试卷(解析版) 题型:填空题
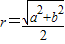 ”.对于“若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c”,类比上述处理方法,可得该三棱锥的外接球半径为R= .
”.对于“若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c”,类比上述处理方法,可得该三棱锥的外接球半径为R= .查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省盐城市大丰市新丰中学高三(上)期中数学试卷(文科)(解析版) 题型:填空题
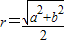 ”.对于“若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c”,类比上述处理方法,可得该三棱锥的外接球半径为R= .
”.对于“若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c”,类比上述处理方法,可得该三棱锥的外接球半径为R= .查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市启东中学高考适应性考试数学试卷(解析版) 题型:解答题
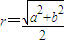 ”.对于“若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c”,类比上述处理方法,可得该三棱锥的外接球半径为R= .
”.对于“若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c”,类比上述处理方法,可得该三棱锥的外接球半径为R= .查看答案和解析>>
科目:高中数学 来源:2010年江苏省盐城市高考数学三模试卷(解析版) 题型:解答题
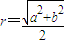 ”.对于“若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c”,类比上述处理方法,可得该三棱锥的外接球半径为R= .
”.对于“若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c”,类比上述处理方法,可得该三棱锥的外接球半径为R= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com