Question

若全集U=R，集合A={x||2x+3|＜5}，B={x|y=log₃（x+2）}，则C_U（A∩B）=（ ）
A．{x|x≤-4或x≥1}
B．{x|x＜-4或x＞1}
C．{x|x＜-2或x＞1}
D．{x|x≤-2或x≥1}

Answer 1

【答案】分析：求出集合A中绝对值不等式的解集，确定出集合A，根据集合B中对数函数的真数大于0，列出关于x的不等式，求出不等式的解集，确定出集合B，找出两集合的公共解集，确定出两集合的交集，根据全集为R，求出交集的补集即可．
解答：解：由集合A中的不等式|2x+3|＜5变形得：-5＜2x+3＜5，
可化为：，
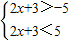
解得：-4＜x＜1，
∴集合A={x|-4＜x＜1}，
由集合B中的函数y=log₃（x+2）有意义，得到x+2＞0，
解得：x＞-2，
∴集合B={x|x＞-2}，
∴A∩B={x|-2＜x＜1}，又全集U=R，
则C_U（A∩B）={x|x≤-2或x≥1}．
故选D
点评：此题属于以绝对值不等式的解法及对数函数的定义域为平台，考查了交、并、补集的混合运算，是高考中常考的基本题型，学生在求补集时注意全集的范围．