
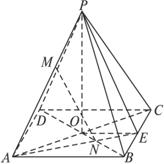
(1)求证:直线MN∥平面PBC;
(2)求直线MN与平面ABCD所成的角.
(1)证明:∵P—ABCD是正四棱锥,
∴ABCD是正方形.连结AN并延长交BC于点E,连结PE.
∵AD∥BC,
∴EN∶AN=BN∶ND.
又∵BN∶ND=PM∶MA,∴EN∶AN=PM∶MA.
∴MN∥PE.
又∵PE在平面PBC内,∴MN∥平面PBC.
(2)解:由(1)知MN∥PE,
∴MN与平面ABCD所成的角就是PE与平面ABCD所成的角.
设点P在底面ABCD上的射影为O,连结OE,则∠PEO为PE与平面ABCD所成的角.
由正棱锥的性质知PO=![]() =
=![]() .
.
由(1)知,BE∶AD=BN∶ND=5∶8,∴BE=![]() .
.
在△PEB中,∠PBE=60°,PB=13,BE=![]() ,
,
根据余弦定理,得PE=![]() .
.
在Rt△POE中,PO=![]() ,PE=
,PE=![]() ,
,
∴sin∠PEO=![]() =
=![]() .
.
故MN与平面ABCD所成的角为arcsin![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
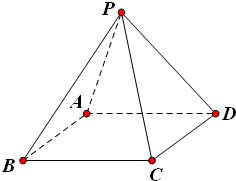 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.查看答案和解析>>
科目:高中数学 来源:2006-2007学年北京市海淀区高三(上)期末数学试卷(理科)(解析版) 题型:填空题
 ,M是侧棱PC的中点,则异面直线PA与BM所成角为 .
,M是侧棱PC的中点,则异面直线PA与BM所成角为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com