练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    学生晓东爱打篮球，假设其每次投篮命中的概率是40%，我们用1，2，3，4表示投中，用5，6，7，8，9，0表示未投中，用计算机随机产生以下20组随机数，可以估计晓东在连续三次投篮中，恰有两次投中的概率是多少？                                （    ）

    812，932，569，683，271，989，730，537，925，264

    907，113，966，191，431，257，393，278，027，556．

    A． 20%             B．25%           C．30%                D．40%

    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    为了某班学生喜爱打篮球是否与性别有关，对本班50人进行问卷调查得到了如下的列联表：
      喜爱打篮球 不喜爱打篮球 合计
    男生 a b=5  
    女生 c=10 d  
    合计     50
    已知在全部50人中随机抽取1人，抽到不爱打篮球的学生的概率为
    2
    5
    ．
    （1）请将上面的列联表补充完整；
    （2）是否有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关；
    请说明理由．
    附参考公式：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ．
    P（ K2≥k） 0.05 0.025 0.010 0.005 0.001
    k 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>

    科目：高中数学 来源：2013届福建省高二下学期第一次月考文科数学试卷（解析版） 题型：解答题

    为了某班学生喜爱打篮球是否与性别有关,对本班50人进行问卷调查得到了如下的列联表:

     已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为.

    (1)请将上面的列联表补充完整;

    (2)是否有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关;请说明理由.

    附参考公式:

    P()

    0.05

    0.025

    0.010

    0.005

    0.001

    k

    3.841

    5.024

    6.635

    7.879

    10.828

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了某班学生喜爱打篮球是否与性别有关，对本班50人进行问卷调查得到了如下的列联表：
    喜爱打篮球不喜爱打篮球合计
    男生ab=5
    女生c=10d
    合计 50
    已知在全部50人中随机抽取1人，抽到不爱打篮球的学生的概率为数学公式．
    （1）请将上面的列联表补充完整；
    （2）是否有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关；
    请说明理由．
    附参考公式：K2=数学公式．
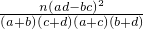    P（ K2≥k）0.050.0250.0100.0050.001
    k3.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源：《统计》2013年高三数学一轮复习单元训练（浙江大学附中）（解析版） 题型：解答题

    为了某班学生喜爱打篮球是否与性别有关，对本班50人进行问卷调查得到了如下的列联表：
     喜爱打篮球不喜爱打篮球合计
    男生ab=5 
    女生c=10d 
    合计  50
    已知在全部50人中随机抽取1人，抽到不爱打篮球的学生的概率为．
    （1）请将上面的列联表补充完整；
    （2）是否有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关；
    请说明理由．
    附参考公式：K2=．
    P（ K2≥k）0.050.0250.0100.0050.001
    k3.8415.0246.6357.87910.828

    查看答案和解析>>

    同步练习册答案