
已知数列{bn}是等差数列b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+![]() )(a>0且a≠1),Sn是数列{an}的前n项和,试比较Sn与
)(a>0且a≠1),Sn是数列{an}的前n项和,试比较Sn与![]() logabn+1大小,并证明你的结论.
logabn+1大小,并证明你的结论.
解:(1)设数列{bn}的公差为d,由题意得
(2)Sn=loga(1+1)+loga(1+ =loga[(1+1)(1+
因此要比较Sn与 当n=1时,1+1=2> n=2时(1+1)(1+ n=3时(1+1)(1+ 由此推测(1+1)(1+ 证明:(1)当n=1时已验证. (2)假设当n=k时(1)式成立 即(1+1)(1+ 则当n=k+1时(1+1)(1+ ∵[ ∴ (1+1)(1+ 即当n=k+1时,(1)式成立. 由(1)、(2)知对于任意正整数都成立. 当a>1时,Sn>
|
通过令n=1,2,3求出a2,a3,a4由此归纳出an再用数学归纳法证明.
|


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a | 2 n+1 |
| a | 2 n |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省南通市启东中学高三考前辅导材料之小题强化篇1(解析版) 题型:解答题
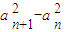 =d(其中d是常数,n∈N﹡),则称数列{an}是“等方差数列”.已知数列{bn}是公差为m的差数列,则m=0是“数列{bn}是等方差数列”的 条件.(填充分不必要、必要不充分、充要条件、既不充分也不必要条件中的一个)
=d(其中d是常数,n∈N﹡),则称数列{an}是“等方差数列”.已知数列{bn}是公差为m的差数列,则m=0是“数列{bn}是等方差数列”的 条件.(填充分不必要、必要不充分、充要条件、既不充分也不必要条件中的一个)查看答案和解析>>
科目:高中数学 来源:2011年江苏省高考数学仿真押题试卷(02)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com