设a∈R,函数f(x)=-(x-1)2+2(a-1)ln(x+1).
(Ⅰ)若函数f(x)在点(0,f(0))处的切线方程为y=4x-1,求a的值;
(Ⅱ)当a<1时,讨论函数f(x)的单调性.
(Ⅰ)解:函数f(x)的定义域为(-1,+∞),
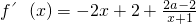
=
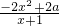
因为f′(0)=4,所以a=2.
(Ⅱ)解:当a<0时,因为x+1>0,-2x
2+2a<0
所以f′(x)<0,故f(x)(-1,+∞)上是减函数;
当a=0时,当x∈(-1,0)时,
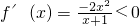
,故f(x)在(-1,0上是减函数,
x∈(0,+∞)时,
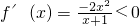
,故f(x)在(0,+∞)上是减函数,
因为函数f(x)在(-1,+∞),上连续,所以f(x)在(-1,+∞),上是减函数;
当0<a<1时,
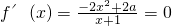
,得x=

,或x=
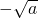
x变化时,f′(x),f(x)的变化如情况下表:
所以f(x)在
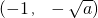
上为减函数、
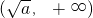
上为减函数;f(x)

上为增函数.(13分)
综上,a≤0时,f(x)在(-1,+∞),上是减函数;
当0<a<1时,f(x)
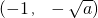
上为减函数、
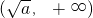
上为减函数;f(x)

上为增函数.
分析:(I)利用导数的几何意义,根据f′(0)=4建立等式关系,求出a的值即可;
(II)根据导数的正负对a进行分类讨论,分别判断出函数的单调性,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可得到答案.
点评:本题主要考查了利用导数研究曲线上某点切线方程的斜率,涉及导数的几何意义,以及函数的单调性等基础题知识,考查运算求解能力、推理论证能力,考查数形结合思想、化归与转化思想、分类讨论的数学思想,属于中档题.

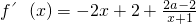 =
=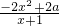
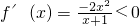 ,故f(x)在(-1,0上是减函数,
,故f(x)在(-1,0上是减函数,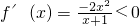 ,故f(x)在(0,+∞)上是减函数,
,故f(x)在(0,+∞)上是减函数,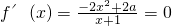 ,得x=
,得x= ,或x=
,或x=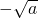
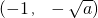
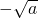


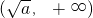
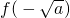
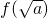
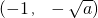 上为减函数、
上为减函数、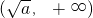 上为减函数;f(x)
上为减函数;f(x) 上为增函数.(13分)
上为增函数.(13分)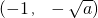 上为减函数、
上为减函数、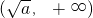 上为减函数;f(x)
上为减函数;f(x) 上为增函数.
上为增函数.

 中考解读考点精练系列答案
中考解读考点精练系列答案