Question

命题p：f（x）=x²+2ax+4，对一切x∈Rf（x）＞0恒成立．q：函数f（x）=（3-2a）^x是增函数，若p或q为真，p且q为假，求实数a的取值范围．

Answer 1

解：因为f（x）=x²+2ax+4，要使对一切x∈R，f（x）＞0恒成立，
即x²+2ax+4＞0对一切x∈R恒成立，
则△=（2a）²-4×1×4=4a²-16＜0恒成立，解得：-2＜a＜2．
所以，命题p为真命题的实数a的取值范围是（-2，2）．
则命题p为假命题的实数a的取值范围是（-∞，-2]∪[2，+∞）．
要使函数f（x）=（3-2a）^x是增函数，
则3-2a＞1，即a＜1．
所以，命题q为真命题的a的取值范围是（-∞，1）．
则命题q为假命题的a的取值范围是[1，+∞）．
若p或q为真，p且q为假，
则p真q假或p假q真．
由p真q假，如图，

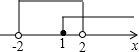
得a的取值范围是[1，2）．
由p假q真，如图，

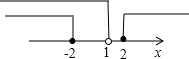
得a的取值范围是（-∞，-2]．
所以，使p或q为真，p且q为假的实数a的取值范围是（-∞，-2]∪[1，2）．
分析：求出对一切x∈R，f（x）＞0恒成立的实数a的取值集合，可以得到命题p为真命题的实数a的取值集合，进一步得到使命题p为假命题的实数a的取值集合；求出使函数f（x）=（3-2a）^x是增函数的实数a的取值集合，可以得到命题q为真命题的取值集合，进一步得到命题q为假命题的取值集合，然后然后根据复合命题的真假，借助于交集运算进行求解．
点评：本题考查了复合命题的真假判断，考查了不等式恒成立问题，训练了补集思想的应用，此题属中档题．