
(本小题分A,B类,满分12分,任选一类,若两类都选,以A类记分)
(A类)已知函数![]() 的图象恒过定点
的图象恒过定点![]() ,且点
,且点![]() 又在函
又在函
数![]() 的图象.
的图象.
(1)求实数![]() 的值; (2)解不等式
的值; (2)解不等式![]()
![]() ;
;
(3)![]() 有两个不等实根时,求
有两个不等实根时,求![]() 的取值范围.
的取值范围.
(B类)设![]() 是定义在
是定义在![]() 上的函数,对任意
上的函数,对任意![]() ,恒有
,恒有
![]() .
.
⑴求![]() 的值; ⑵求证:
的值; ⑵求证:![]() 为奇函数;
为奇函数;
⑶若函数![]() 是
是![]() 上的增函数,已知
上的增函数,已知![]() 且
且![]() ,求
,求![]() 的
的
取值范围.
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源:2010-2011年广东省广州市高一下学期期末考试数学 题型:解答题
(本小题满分14分)
某工厂生产A、B型两类产品,每个产品需粗加工和精加工两道工序完成. 已知粗加工做一个A、B型产品分别需要1小时和2小时,精加工一个A、B型产品分别需要3小时和1小时;又知粗加工、精加工每天工作分别不得超过8小时和9小时,而工厂生产一个A、B型产品分别获利润200元和300元,试问工厂每天应生产A、B型产品各多少个,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省皖南八校高三第一次联考文科数学试卷解析版 题型:解答题
(本小题满分12分)某汽车厂生产A、B两类轿车,每类轿车均有舒适型和标准型两种,某月的产量如下表:

按分层抽样的方法在该月生产的轿车中抽取50辆,其中A类轿车20辆。
(I)求x的值;
(II)用分层抽样的方法在B类轿车中抽取一个容量为6的样本,从样本中任意取2辆,求至少有一辆舒适轿车的概率。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省宁波市高三高考理数模拟试题 题型:解答题
(本小题满分14分)
函数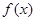 定义在区间[a, b]上,设“
定义在区间[a, b]上,设“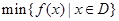 ”表示函数
”表示函数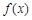 在集合D上的最小值,“
在集合D上的最小值,“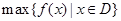 ”表示函数
”表示函数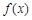 在集合D上的最大值.现设
在集合D上的最大值.现设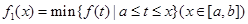 ,
,
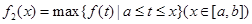 ,
,
若存在最小正整数k,使得 对任意的
对任意的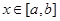 成立,则称函数
成立,则称函数
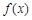 为区间
为区间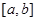 上的“第k类压缩函数”.
上的“第k类压缩函数”.
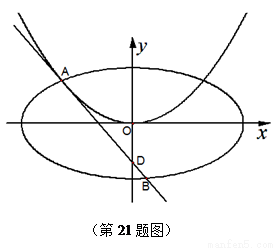
(Ⅰ) 若函数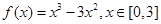 ,求
,求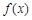 的最大值,写出
的最大值,写出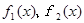 的解析式;
的解析式;
(Ⅱ) 若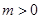 ,函数
,函数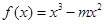 是
是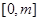 上的“第3类压缩函数”,求m的取值范围.
上的“第3类压缩函数”,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011年河北冀州中学高一年级下学期期末考试文科数学(A卷) 题型:解答题
(本小题满分12分)某工厂家具车间造A,B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A,B型桌子分别需要1 h和2 h,漆工油漆一张A,B型桌子分别需要3 h和1 h;又知木工、漆工每天工作分别不得超过8 h和9 h,而工厂造一张A,B型桌子分别获利润2千元和3千元,试问:工厂每天应生产A,B型桌子各多少张,才能获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com