
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°AB=AC=2,AA1=3.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°AB=AC=2,AA1=3.分析 (Ⅰ)利用勾股定理求解三角形的边长,推出P的位置.
(Ⅱ)求出四棱锥P-BCC1B1与三棱柱ABC-A1B1C1的体积,即可得到比值.
解答 解:(Ⅰ)由题意$PC=PB=2\sqrt{2}$,(2分)
在三棱柱中,由AA1⊥平面ABC,且AB=AC=2
可得:PA=2,(4分)
故点P的位置为AA1的三等分点,且靠近A1处. (6分)
(Ⅱ)由(Ⅰ)可知,${V_{ABC-{A_1}{B_1}{C_1}}}=\frac{1}{2}×2×2×3=6$,(7分)
${V_{P-{A_1}{B_1}{C_1}}}=\frac{1}{3}×\frac{1}{2}×2×2×1=\frac{2}{3}$(8分)
${V_{P-ABC}}=\frac{1}{3}×\frac{1}{2}×2×2×2=\frac{4}{3}$,(9分)
所以${V_{P-BC{C_1}{B_1}}}=6-\frac{4}{3}-\frac{2}{3}=4$,
所以所求两个几何体的体积比为$\frac{2}{3}$. (12分)
故答案为:(Ⅰ)点P的位置为AA1的三等分点,且靠近A1处;(Ⅱ)体积比为$\frac{2}{3}$.
点评 本题考查几何体的体积的计算,直线与平面垂直的性质的应用,判断计算能力.


科目:高中数学 来源: 题型:选择题
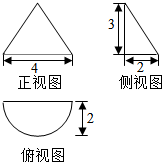
| A. | $(4+2\sqrt{13})π$ | B. | $6+(2+\sqrt{13})π$ | C. | $(\sqrt{13}+2)π$ | D. | $8+2\sqrt{13}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.
如图,在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4) | B. | (-4,0) | C. | $(0,\frac{15}{4})$ | D. | $(\frac{1}{2},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com