
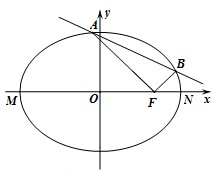
 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| x |
| a |
| y |
| b |
| c |
| a |
| ||
| 3 |
| |bc| | ||
|
|
| ||
| 3 |
| c |
| a |
| ||
| 3 |
| ||
| 3 |
| x |
| a |
| y |
| b |
| |bc| | ||
|
| x2 |
| 6 |
| y2 |
| 2 |
|
| 6kb |
| 1+3k2 |
| 3b2-6 |
| 1+3k2 |
| y1 |
| x1-2 |
| y2 |
| x2-1 |
| 3b2-6 |
| 1+3k2 |
| -6kb |
| 1+3k2 |


科目:高中数学 来源: 题型:
| x2 |
| 5 |
| y2 |
| m |
| x2 |
| 3 |
| y2 |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+2x |
| x2-x |
| x+1 |
| x+2 |
| x2-1 |
| x2+1 |
| 3x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| AQ |
| QB |
| NQ |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在学习完统计学知识后,两位同学对所在年级的1200名同学一次数学考试成绩作抽样调查,两位同学采用简单随机抽样方法抽取100名学生的成绩,并将所选的数学成绩制成如下统计表,设本次考试的最低期望分数为90分,优等生最低分130分,并且考试成绩分数在[85,90)的学生通过自身努力能达到最低期望分数.
在学习完统计学知识后,两位同学对所在年级的1200名同学一次数学考试成绩作抽样调查,两位同学采用简单随机抽样方法抽取100名学生的成绩,并将所选的数学成绩制成如下统计表,设本次考试的最低期望分数为90分,优等生最低分130分,并且考试成绩分数在[85,90)的学生通过自身努力能达到最低期望分数.| 分数段 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 9 | 6 | 12 | 18 | 21 | 16 | 12 | 6 |
| 频率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com