
| AC |
| m |
| BD |
| n |
| m |
| n |
| AB |
| AD |
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:北京高考真题 题型:解答题
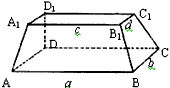
 (S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。查看答案和解析>>
科目:高中数学 来源:北京高考真题 题型:解答题
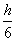 (S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。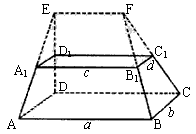
查看答案和解析>>
科目:高中数学 来源: 题型:
一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;…;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若![]() ,
,![]() ,则称矩形ABCD为2阶奇异矩形.
,则称矩形ABCD为2阶奇异矩形.

(1)判断与操作:
如图2,矩形ABCD长为5,宽为2,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
(2)探究与计算:
已知矩形ABCD的一边长为20,另一边长为![]() (a < 20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出
(a < 20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出![]() 的值.
的值.
(3)归纳与拓展:
已知矩形ABCD两邻边的长分别为b,c(b < c),且它是4阶奇异矩形,求b︰c(直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com