
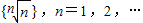 ,则数列中最大项的值为 .
,则数列中最大项的值为 . 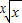 ,(x>0),则lny=
,(x>0),则lny= lnx,再设F(x)=lny=
lnx,再设F(x)=lny=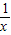 lnx,求导数F′(x)=-
lnx,求导数F′(x)=-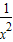 lnx+
lnx+ =
=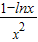 ,利用导数研究它的单调性,得出F(x)在区间[3,+∞)是减函数,在(0,2]是增函数,又由于
,利用导数研究它的单调性,得出F(x)在区间[3,+∞)是减函数,在(0,2]是增函数,又由于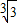 >
>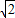 ,从而得出数列中最大项的值.
,从而得出数列中最大项的值.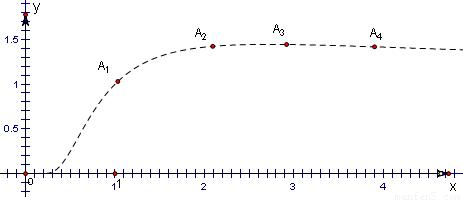 解:设y=
解:设y=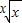 ,(x>0),
,(x>0),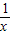 lnx,
lnx,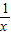 lnx,
lnx, lnx+
lnx+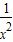 =
=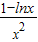 ,
,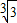 >
>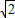 ,
,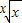 的最大值为
的最大值为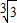 .
.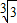 .
.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com