
分析 由题意,OA⊥OB,|OB|=2|OA|,可得∠AOB=60°,利用$\frac{b}{a}$=tan∠AOF=tan30°=$\frac{\sqrt{3}}{3}$,e=$\sqrt{1+(\frac{b}{a})^{2}}$,即可求出双曲线C的离心率.
解答 解:由题意,OA⊥aB,|OB|=2|OA|,
∴∠AOB=60°,
∴∠AOF=30°,
∴$\frac{b}{a}$=tan∠AOF=tan30°=$\frac{\sqrt{3}}{3}$,
∴e=$\sqrt{1+(\frac{b}{a})^{2}}$=$\frac{{2\sqrt{3}}}{3}$.
故答案为:$\frac{{2\sqrt{3}}}{3}$.
点评 本题考查双曲线C的离心率,考查特殊角的三角函数,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3074 | B. | 2065 | C. | 2024 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .$(2,\frac{10}{3})$ | B. | $(-∞,\frac{10}{3})$ | C. | $[2,\frac{10}{3}]$ | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
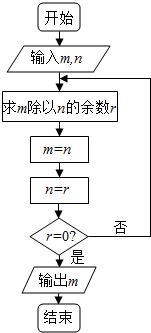 如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )
如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )| A. | 0 | B. | 2 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com