

| A. | $\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | B. | -$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$ | C. | -$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | D. | 3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$ |
分析 以 $\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$互相垂直的单位向量所在的直线分别为x轴和y轴,建立直角坐标系,求出向量$\overrightarrow{a}$ 的终点坐标以及$\overrightarrow{b}$的终点坐标,即可得到结论..
解答 解:以 $\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$互相垂直的单位向量所在的直线分别为x轴和y轴,建立直角坐标系,
则$\overrightarrow{{e}_{1}}$=(1,0),$\overrightarrow{{e}_{2}}$=(0,1),
则向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(1,-2),$\overrightarrow{c}$=(1,2),
则向量$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$=(1,2)+(1,-2)-(1,2)=(1,-2),
即可表示为$\overrightarrow{{e}_{1}}$-2 $\overrightarrow{{e}_{2}}$,
故选:A.
点评 本题考查两个向量的加减法的法则,以及其几何意义,向量坐标的运算,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (2,+∞) | C. | (-2,1)∪(2,+∞) | D. | (-∞,-2)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
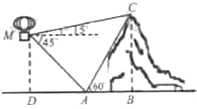 如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知∠BAC=60°,则山的高度BC为( )
如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知∠BAC=60°,则山的高度BC为( )| A. | 700 m | B. | 640 m | C. | 600 m | D. | 560 m |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com